如图:由于过渡采伐森林和破坏植被,使我国某些地区多次受到沙尘暴的侵袭.近来A市气象局测得沙尘暴中心在A市正东方向400km的B处,正在向西北方向移动,距沙尘暴中心300km的范围内将受到影响,问A市是否会受到这次沙尘暴的影响?
阅读与理解
在平面直角坐标系xoy中,点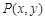 经过
经过 变换得到点
变换得到点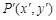 ,该变换记为
,该变换记为 ,其中
,其中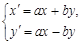
 为常数
为常数 .
.
例如,当 ,且
,且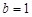 时,
时, .
.
(1) 当 ,且
,且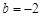 时,
时,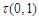 = ;
= ;
(2) 若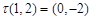 ,则
,则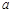 = ,
= ,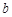 = ;
= ;
(3) 设点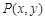 是直线
是直线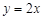 上的任意一点,点
上的任意一点,点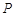 经过变换
经过变换 得到点
得到点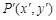 .若点
.若点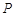 与点
与点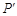 关于原点对称,求
关于原点对称,求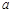 和
和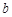 的值.
的值.
一船在A处测得北偏东60°方向有一灯塔B,船向正东方向以每小时20海里的速度航行1.5小时到达C处时,又观测到灯塔B在北偏东15°方向上,求此时航船与灯塔相距多少海里?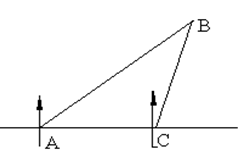
(本题9分)小明平时喜欢玩 “QQ农场”游戏,本学期八年级数学备课组组织了几次数学反馈性测试,小明的数学成绩如下表:
| 月份x(月) |
9 |
10 |
11 |
12 |
|
| 成绩y |
90 |
80 |
70 |
60 |
|
(1)以月份为x轴,成绩为y轴,根据上表提供的数据在下面的直角坐标系中描点;
(2)观察①中所描点的位置关系,猜想y与x之间的函数关系,并求出所猜想的函数关系式;
(3)若小明继续沉溺于“QQ农场”游戏,照这样的发展趋势,请你估计元月份的期末考试中小明的数学成绩,并用一句话对小明提出建议.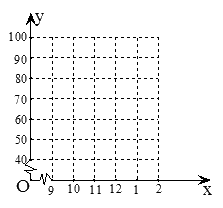
(1)在图1中,平行四边形ABCD的顶点A,B,C,D的坐标(如图),请写出图中的顶点C的坐标( _________ , _________ ).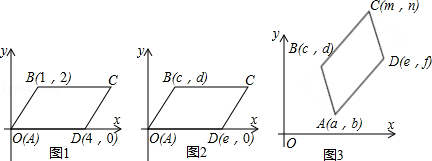
(2)在图2中,平行四边形ABCD的顶点A,B,C,D的坐标(如图),求出图中的标点C的坐标,并说明理由(C点坐标用含c,d,e的代数式表示).
归纳与发现
(3)通过对图1,2的观察,你会发现:图3中的平行四边形ABCD的顶点坐标为A(a,b),B(c,d),C(m,n),D(e,f)时,则横坐标a,c,m,e之间的等量关系为 _________ .
对某一个函数给出如下定义:若存在实数 ,对于任意的函数值
,对于任意的函数值 ,都满足
,都满足 ,则称这个函数是有界函数,在所有满足条件的
,则称这个函数是有界函数,在所有满足条件的 中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.
中,其最小值称为这个函数的边界值.例如,下图中的函数是有界函数,其边界值是1.
(1)分别判断函数
 和
和 是不是有界函数?若是有界函数,求其边界值;
是不是有界函数?若是有界函数,求其边界值;
(2)若函数
 的边界值是2,且这个函数的最大值也是2,求
的边界值是2,且这个函数的最大值也是2,求 的取值范围;
的取值范围;
(3)将函数 的图象向下平移
的图象向下平移 个单位,得到的函数的边界值是
个单位,得到的函数的边界值是 ,当
,当 在什么范围时,满足
在什么范围时,满足 ?
?
已知动点P以每秒2cm的速度沿如图所示的边框按从B⇒C⇒D⇒E⇒F⇒A的路径移动,相应的△ABP的面积S关于时间t的函数图象如图所示,若AB=6cm,试回答下列问题:
(1)动点P在线段 上运动的过程中△ABP的面积S保持不变.
(2)BC= cm; CD= cm; DE= cm; EF= cm
(3)求出图乙中的a与b的值.
某天早晨,小王从家出发,骑摩托车前往工厂上班,途中在路旁一家饭店吃早餐,如图所示的是小王从家到工厂这一过程中行驶路程 s(千米)与时间t之间的关系.
(1)工厂离小王家多远?从家出发到工厂,小王共用了多少时间?
(2)小王吃早餐用了多少时间?
(3)小王吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?
如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别为A(﹣1,2),B(﹣3,4)C(﹣2,6)
(1)画出△ABC绕点A顺时针旋转90°后得到的△A1B1C1
(2)以原点O为位似中心,画出将△A1B1C1三条边放大为原来的2倍后的△A2B2C2.
如图1,菱形ABCD中,∠A=60°,点P从A出发,以2cm/s的速度沿边AB、BC、CD匀速运动到D终止,点Q从A与P同时出发,沿边AD匀速运动到D终止,设点P运动的时间为t(s).△APQ的面积S(cm2)与t(s)之间函数关系的图象由图2中的曲线段OE与线段EF、FG给出.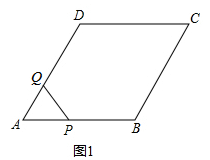

(1)求点Q运动的速度;
(2)求图2中线段FG的函数关系式;
(3)问:是否存在这样的t,使PQ将菱形ABCD的面积恰好分成1:5的两部分?若存在,求出这样的t的值;若不存在,请说明理由.
在平面直角坐标系xOy中,已知A(-1,5),B(4,2),C(-1,0)三点。
(1)点A关于原点O的对称点A′的坐标为 ,点B关于x轴对称点B′的坐标为 ,点C关于y轴对称点C′的坐标为 ;
(2)求(1)中的△A′B′C′的面积。
如图,Rt△ABO的顶点A是双曲线y= 与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且
与直线y=-x-(k+1)在第二象限的交点.AB⊥x轴于B,且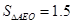 .
.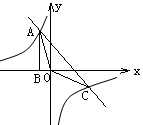
(1)求这两个函数的解析式;
(2)求直线与双曲线的两个交点A、C的坐标和△AOC的面积.并根据图像写出;
(3)方程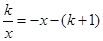 的解;
的解;
(4)使一次函数的值大于反比例函数的值的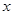 的取值范围;
的取值范围;