江苏省盐城市盐都区八年级上学期期末考试数学试卷
如图,小手盖住的点的坐标可能为 ( )
| A.(4,3) | B.(-4,3) | C.(-4,-3) | D.(4,-3) |
以下列各组数为边长,能构成直角三角形的是( )
| A.1,2,3 | B. , , , , |
C. , , , , |
D.3, 4, 5 |
李大爷要围成一个矩形菜园,菜园的一边利用足够长的墙,用篱笆围成的另外三边总长度恰好为24米.要围成的菜园是如图所示的长方形ABCD.设BC边的长为x米,AB边的长为y米,则y与x之间的函数关系式是( )
A. B.
B.
C. D.
D.
一次函数 经过第一、二、四象限,则下列正确的是( )
经过第一、二、四象限,则下列正确的是( )
| A.k>0,b>0 | B.k>0,b<0 |
| C.k<0,b>0 | D.k<0,b<0 |
如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是 ( )
| A.∠B=∠D=90° | B.∠BCA=∠DCA |
| C.∠BAC=∠DAC | D.CB=CD |
如图,在锐角△ABC中,AB= ,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
,∠BAC=45°,∠BAC的平分线交BC于点D,M、N分别是AD和AB上的动点,则BM+MN的最小值是( )
A. |
B.1 | C. |
D. |
将函数 的图像向上平移1个单位长度后得到的图像所对应的函数关系式是_________.
的图像向上平移1个单位长度后得到的图像所对应的函数关系式是_________.
“任意打开一本200页的数学书,正好是第20页”,这是 事件(选填“随机”或“必然”).
口袋内装有一些除颜色外完全相同的3个红球、2个白球.从中任意摸出一个球,那么摸出_______球(填“红”或“白”)的概率大.
在一次函数 的图象中,y随x的增大而增大.则满足条件的k值可以是_______.(写出一个即可)
的图象中,y随x的增大而增大.则满足条件的k值可以是_______.(写出一个即可)
在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是实验中的一组统计数据:
(1)请估计:当 很大时,摸到白球的频率将会接近 .(精确到0.1)
很大时,摸到白球的频率将会接近 .(精确到0.1)
(2)假如你摸一次,你摸到白球的概率 .
.
(3)试估算盒子里黑、白两种颜色的球各有多少只?
在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.
(1)求证:Rt△ABE≌Rt△CBF;
(2)若∠CAE=30°,求∠ACF度数.
如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在BC边上,且∠GDF=∠ADF.
(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系,并说明理由.
某公园元旦期间,前往参观的人非常多.这期间某一天某一时段,随机调查了部分入园游客,统计了他们进园前等候检票的时间,并绘制成如下图表.表中“10~20”表示等候检票的时间大于或等于10min而小于20min,其它类同.
(1)这里采用的调查方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)表中a=____,b=_____,并请补全频数分布直方图;
(3)在调查人数里,若将时间分段内的人数绘成扇形统计图,则“40~50”的圆心角的度数是 .
小聪和小明沿同一条路同时从学校出发到市图书馆查阅资料,小聪骑电动车,小明骑自行车,当小聪从原路回到学校时,小明刚好到市图书馆,图中折线O﹣A﹣B﹣C和线段OD分别表示两人离学校的路程s(千米)与所经过的时间t(小时)之间的函数关系,请根据图象回答下列问题:
(1)学校到市图书馆的路程是 千米,小聪在市图书馆查阅资料的时间为 小时;
(2)小明骑自行车的速度是 千米/小时;
(3)请你求出小聪返回学校过程中,路程s(千米)与所经过的时间t(小时)之间的函数关系式.
Rt△ABC中,AB=6,∠ACB=60°,∠ABC=90°.建立如图所示的平面直角坐标系xOy(点B与原点O重合,点C在x轴上).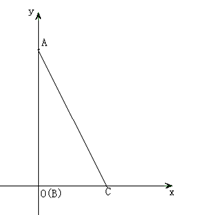
(1)写出点A的坐标;
(2)在AB上求作一点D,使点D到AC两端点的距离相等.(不写作法,保留作图痕迹)
(3)在(2)中,求点D的坐标.
阅读与理解
在平面直角坐标系xoy中,点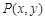 经过
经过 变换得到点
变换得到点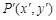 ,该变换记为
,该变换记为 ,其中
,其中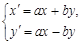
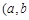 为常数
为常数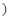 .
.
例如,当 ,且
,且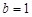 时,
时, .
.
(1) 当 ,且
,且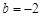 时,
时,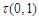 = ;
= ;
(2) 若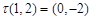 ,则
,则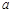 = ,
= ,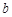 = ;
= ;
(3) 设点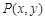 是直线
是直线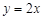 上的任意一点,点
上的任意一点,点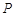 经过变换
经过变换 得到点
得到点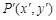 .若点
.若点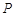 与点
与点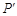 关于原点对称,求
关于原点对称,求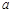 和
和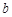 的值.
的值.
【问题情境】
徐老师给爱好学习的小敏和小捷提出这样一个问题:
如图1,△ABC中,∠B=2∠C,AD是∠BAC的平分线.求证:AB+BD=AC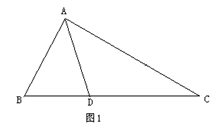
小敏的证明思路是:在AC上截取AE=AB,
连接DE.(如图2)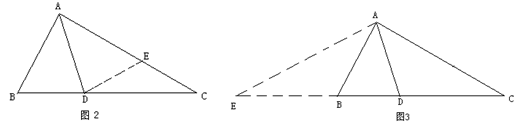
小捷的证明思路是:延长CB至点E,使BE=AB,连接AE.可以证得:AE=DE(如图3)
请你任意选择一种思路继续完成下一步的证明.
【变式探究】
“AD是∠BAC的平分线”改成“AD是BC边上的高”,其它条件不变.(如图4)
AB+BD=AC成立吗?若成立,请证明;若不成立,写出你的正确结论,并说明理由.
【迁移拓展】
△ABC中,∠B=2∠C.求证: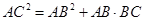 .(如图5)
.(如图5)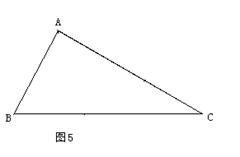




 ,0,
,0, ,
, ,
, 中,无理数有( )
中,无理数有( ) __________2.(填“>”、“=”、“<”)
__________2.(填“>”、“=”、“<”)
 与
与 的图像交于点P(m,2),则不等式
的图像交于点P(m,2),则不等式 的解集为 .
的解集为 .
 的值:(1)
的值:(1)

 粤公网安备 44130202000953号
粤公网安备 44130202000953号