在平面直角坐标系中,将三角形各点的纵坐标都减去3,横坐标保持不变,所得
图形与原图形相比是( ).
| A.向右平移了3个单位 | B.向左平移了3个单位 |
| C.向上平移了3个单位 | D.向下平移了3个单位 |
若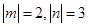 ,则点A(
,则点A(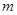 ,
,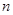 ) ( )
) ( )
| A.四个象限均有可能 | B.在第一象限或第三象限或第四象限 |
| C.在第一象限或第二象限 | D.在第二象限或第三象限或第四象限 |
在平面直角坐标系中,下面的点在第一象限的是
| A. | (1,2) | B. | (-2,3) | C. | (0,0) | D. | (-3,-2) |
小明用计算器计算 的值,其按键顺序和计算器显示结果如表:

这时他才明白计算器是先做乘法再做加法的,于是他依次按键:

从而得到了正确结果,已知 是 的3倍,则正确的结果是
A.24B.39C.48D.96
如图,若将直角坐标系中“鱼”的每个“顶点”的横坐标保持不变,纵坐标分别变为原来的,则点A的对应点的坐标是【 】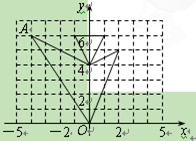
| A.(-4,3) | B.(4,3) | C.(-2,6) | D.(-2,3) |
若 轴上的点P到
轴上的点P到 轴的距离为5,则点P的坐标为( )
轴的距离为5,则点P的坐标为( )
| A.(0,5) | B.(0,5)或(0,–5) |
| C.(5,0) | D.(5,0)或(–5,0) |
早晨,小张去公园晨练,下图是他离家的距离y(千
米)与时间t(分钟)的函数图象,根据图象信息,下列说法正确的是 ( )
| A.小张去时所用的时间多于回家所用的时间 | B.小张在公园锻炼了20分钟 |
| C.小张去时的速度大于回家的速度 | D.小张去时走上坡路,回家时走下坡路 |
如图4,AD、BC是⊙O的两条互相垂直的直径,点P从点O出发,沿O→C→D→O的路线匀速运动,设∠APB=y(单位:度),那么y与点P运动的时间x(单位:秒)的关系图是( )

利用计算器求值时,小明将按键顺序为 显示结果记为
,
显示结果记为
,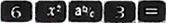 的显示结果记为
.则
,
的大小关系为
的显示结果记为
.则
,
的大小关系为
A. B. C. D.不能比较
函数y=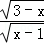 中x的取值范围是( )
中x的取值范围是( )
| A.x≤3 | B.x≠1 | C.x≤3且x≠1 | D.1<x≤3 |
如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路线为x,以点A、P、D为顶点的三角形的面积是y.则下列图象能大致反映y与x的函数关系的是( )


下列平面直角坐标系中的曲线,不能表示 是
是 的函数的是( ).
的函数的是( ).
小明从家骑车上学,先上坡到达A地后再下坡到达学校,所用的时间与路程如图所示.如果返回时,上、下坡的速度仍然保持不变,那么他从学校回到家需要的时间是( )
| A.8.6分钟 | B.9分钟 | C.12分钟 | D.16分钟 |
