在平面直角坐标系中,将抛物线y=x2+2x+3绕着它与y轴的交点旋转180°,所得抛物线的解析式是( )
| A.y=﹣(x+1)2+2 | B.y=﹣(x﹣1)2+4 |
| C.y=﹣(x﹣1)2+2 | D.y=﹣(x+1)2+4 |
如图是某蓄水池的横断面示意图,分为深水池和浅水池,如果这个蓄水池以固定的流量注水,下面能大致表示水的最大深度h与时间t之间的关系的图象是( )

如图,若在象棋盘上建立直角坐标系,使“帅”位于点
 .“馬”位于点
.“馬”位于点 ,则“兵”位于点( )
,则“兵”位于点( )
A. |
B. |
C. |
D. |
在平面直角坐标系中,设点P到原点O的距离为p,OP与x轴正方向的夹角为a,则用[p,α]表示点P的极坐标,显然,点P的极坐标与它的坐标存在一一对应关系.例如:点P的坐标为(1,1),则其极坐标为[ ,45°].若点Q的极坐标为[4,60°],则点Q的坐标为( )
,45°].若点Q的极坐标为[4,60°],则点Q的坐标为( )
A.(2, ) ) |
B.(2, ) ) |
C.( ,2) ,2) |
D.(2,2) |
如图,正方形ABCD的边长为a,动点P从点A出发,沿折线A→B→D→C→A的路径运动,回到点A时运动停止.设点P运动的路程长为长为x,AP长为y,则y关于x的函数图象大致是( )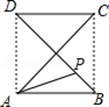

如图,△ABC中,∠C = 90°,M是AB的中点,动点P从点A出发,沿AC方向匀速运动到终点C,动点Q从点C出发,沿CB方向匀速运动到终点B.已知P,Q两点同时出发,并同时到达终点,连接MP,MQ,PQ .在整个运动过程中,△MPQ的面积大小变化情况是( )
A.一直增大 B.一直减小
C.先减小后增大 D.先增大后减小
利用计算器求值时,小明将按键顺序为 显示结果记为
,
显示结果记为
,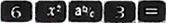 的显示结果记为
.则
,
的大小关系为
的显示结果记为
.则
,
的大小关系为
A. B. C. D.不能比较
函数y=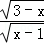 中x的取值范围是( )
中x的取值范围是( )
| A.x≤3 | B.x≠1 | C.x≤3且x≠1 | D.1<x≤3 |
如图,正方形ABCD的边长为4,P为正方形边上一动点,运动路线是A→D→C→B→A,设P点经过的路线为x,以点A、P、D为顶点的三角形的面积是y.则下列图象能大致反映y与x的函数关系的是( )


下列平面直角坐标系中的曲线,不能表示 是
是 的函数的是( ).
的函数的是( ).
小明从家骑车上学,先上坡到达A地后再下坡到达学校,所用的时间与路程如图所示.如果返回时,上、下坡的速度仍然保持不变,那么他从学校回到家需要的时间是( )
| A.8.6分钟 | B.9分钟 | C.12分钟 | D.16分钟 |
