设点 和
和 是反比例函数
是反比例函数 图象上的两个点,当
图象上的两个点,当 <
< <
< 时,
时, <
< ,则一次函数
,则一次函数 的图象不经过的象限是
的图象不经过的象限是
| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
如图,港口A在观测站O的正东方向,OA="4" km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船航行的距离(即AB的长)为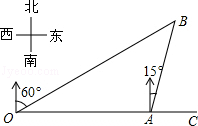
| A.4km | B. km km |
C.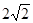 km km |
D.( km km |
在同一直线坐标系中,若正比例函数y=k1x的图像与反比例函数 的图像没有公共点,则
的图像没有公共点,则
| A.k1+k2<0 | B.k1+k2>0 | C.k1k2<0 | D.k1k2>0 |
小明用计算器计算 的值,其按键顺序和计算器显示结果如表:

这时他才明白计算器是先做乘法再做加法的,于是他依次按键:

从而得到了正确结果,已知 是 的3倍,则正确的结果是
A.24B.39C.48D.96
如图,点P是以O为圆心,AB为直径的半圆上的动点,AB=2,设弦AP的长为x,△APO的面积为y,则下列图象中,能表示y与x的函数关系的图象大致是
A. |
B. |
C. |
D. |
阅读下面材料:
小红遇到这样一个问题:如图1,在四边形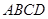 中,
中,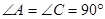 ,
,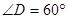 ,
,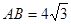 ,
, ,求
,求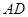 的长.
的长.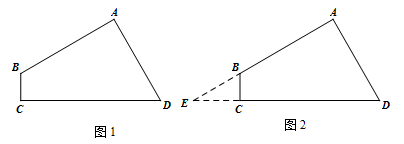
小红发现,延长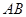 与
与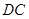 相交于点
相交于点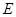 ,通过构造Rt△
,通过构造Rt△ ,经过推理和计算能够使问题得到解决(如图2).
,经过推理和计算能够使问题得到解决(如图2).
(1)请回答: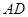 的长为 .
的长为 .
(2)参考小红思考问题的方法,解决问题:
如图3,在四边形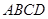 中,
中, ,
,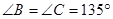 ,
,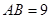 ,
, ,求
,求 和
和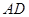 的长.
的长.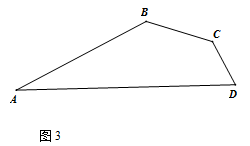
如图是丁丁画的一张脸的示意图,如果用(0,2)表示左眼,用(2,2)表示右眼,那么嘴的位置可以表示成( )
| A.(1,0) | B.(-1,0) | C.(-1,1) | D.(1,-1) |
芳芳用水管以均匀的速度向一个容器中注水,在注水过程中,水面的高度h与注水时间t之间的函数图象如图所示,最后芳芳将容器注满水,则这个容器的形状大致为( )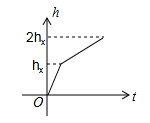
利用计算器求值时,小明将按键顺序为 显示结果记为
,
显示结果记为
,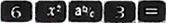 的显示结果记为
.则
,
的大小关系为
的显示结果记为
.则
,
的大小关系为
A. B. C. D.不能比较
函数y=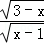 中x的取值范围是( )
中x的取值范围是( )
| A.x≤3 | B.x≠1 | C.x≤3且x≠1 | D.1<x≤3 |
如图,在一个18米高的楼顶上有一信号塔DC,李明同学为了测量信号塔的高度,在地面的A处测的信号塔下端D的仰角为30°,然后他正对塔的方向前进了18米到达地面的B处,又测得信号塔顶端C的仰角为60°,CD⊥AB与点E,E、B、A在一条直线上.请你帮李明同学计算出信号塔CD的高度(结果保留整数, ≈1.7,
≈1.7, ≈1.4 )
≈1.4 )