阅读理解:
材料一:若三个非零实数 , , 满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数 , , 构成"和谐三数组".
材料二:若关于 的一元二次方程 的两根分别为 , ,则有 , .
问题解决:
(1)请你写出三个能构成"和谐三数组"的实数 ;
(2)若 , 是关于 的方程 , , 均不为 的两根, 是关于 的方程 , 均不为 的解.求证: , , 可以构成"和谐三数组";
(3)若 , , 三个点均在反比例函数 的图象上,且三点的纵坐标恰好构成"和谐三数组",求实数 的值.
阅读理解:
材料一:若三个非零实数 , , 满足:只要其中一个数的倒数等于另外两个数的倒数的和,则称这三个实数 , , 构成"和谐三数组".
材料二:若关于 的一元二次方程 的两根分别为 , ,则有 , .
问题解决:
(1)请你写出三个能构成"和谐三数组"的实数 ;
(2)若 , 是关于 的方程 , , 均不为 的两根, 是关于 的方程 , 均不为 的解.求证: , , 可以构成"和谐三数组";
(3)若 , , 三个点均在反比例函数 的图象上,且三点的纵坐标恰好构成"和谐三数组",求实数 的值.
如果关于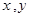 的单项式
的单项式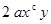 与单项式
与单项式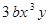 是同类项,并且
是同类项,并且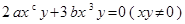 ,当m 的倒数是-1,n的相反数是
,当m 的倒数是-1,n的相反数是 时,求
时,求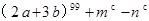 的值。
的值。
已知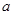 、
、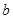 互为相反数且
互为相反数且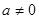 ,
, 、
、 互为倒数,
互为倒数,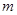 的绝对值是最小的正整数,
的绝对值是最小的正整数,
求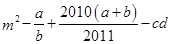 的值. (注:
的值. (注: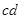 =
=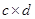 )
)
解:∵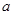 、
、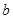 互为相反数且
互为相反数且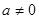 , ∴
, ∴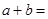 __________,
__________, __________;
__________;
又∵ 、
、 互为倒数,∴
互为倒数,∴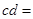 __________;
__________;
又∵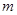 的绝对值是最小的正整数, ∴
的绝对值是最小的正整数, ∴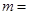 __________,∴
__________,∴ __________;
__________;
∴原式 __________.
__________.
列式并计算:
(1)﹣1减去 的差乘以﹣7的倒数的积;
的差乘以﹣7的倒数的积;
(2)﹣2、5、﹣9这三个数的和的绝对值比这三个数的绝对值的和小多少?
已知a的相反数为-2,b的倒数为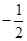 ,c的绝对值为2,求a+b+c2的值.
,c的绝对值为2,求a+b+c2的值.
已知: 与
与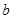 互为相反数,
互为相反数,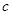 与
与 互为倒数,当
互为倒数,当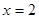 时,求代数式
时,求代数式 的值.
的值.
已知a,b互为相反数,c,d互为倒数,x的绝对值为5,试求:(a+b+cd)x2+(a+b)2008-(-cd)2015的值.