(本题14分)如图,在平面直角坐标系中,直线AB与x轴交于点A(4,0),与y轴交于点B(0,4),抛物线 的的顶点为E.点C的坐标为(0,m)(m≠4),点C关于AB的对称点是点D,连结BD,CD,CE,DE
的的顶点为E.点C的坐标为(0,m)(m≠4),点C关于AB的对称点是点D,连结BD,CD,CE,DE

(1)当点C在线段OB上时,求证:△BCD是等腰直角三角形;
(2)当m>0时,若△CDE为直角三角形,求tan∠CEO的值;
(3)设点P是该抛物线上一点,是否存在m的值,使以P,C,D,E为顶点的四边形为平行四边形,若存在,请直接写出所有满足条件的m的值;若不存在,请说明理由.
“校园手机”现象越来越受到社会的关注.小丽在“统计实习”活动中随机调查了学校若干名学生家长对“中学生带手机到学校”现象的看法,统计整理并制作了如下的统计图: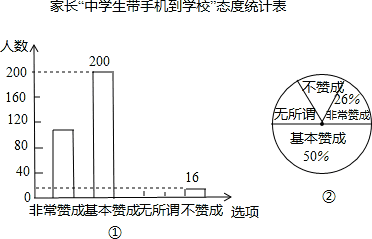
(1)求这次调查的家长总数及家长表示“无所谓”的人数,并补全图①;
(2)求图②中表示家长“无所谓”的圆心角的度数;
(3)从这次接受调查的家长中,随机抽查一个,恰好是“不赞成”态度的家长的概率是多少?
小晗家客厅里装有一种三位单极开关,分别控制着A(楼梯)、B(客厅)、C(走廊)三盏电灯,在正常情况下,小晗按下任意一个开关均可打开对应的一盏电灯,既可三盏、两盏齐开,也可分别单盏开.因刚搬进新房不久,不熟悉情况.
(1)若小晗任意按下一个开关,正好楼梯灯亮的概率是多少?
(2)若任意按下其中的两个开关,则正好客厅灯和走廊灯同时亮的概率是多少?请用树状图或列表加以说明.
如图,在平面直角坐标系xoy中,点O为坐标原点,抛物线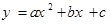 与x轴交于点A(
与x轴交于点A( ,0)、B(2,0),与y轴交于点C,以O为圆心,半径为1的⊙O恰好经过点C,与x轴的正半轴交于点D.
,0)、B(2,0),与y轴交于点C,以O为圆心,半径为1的⊙O恰好经过点C,与x轴的正半轴交于点D.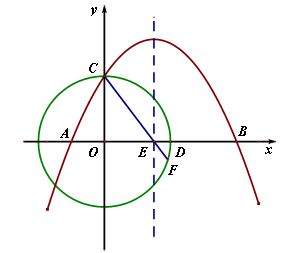
(1)求抛物线相应的函数表达式;
(2)抛物线的对称轴交x轴于点E,连结CE,并延长CE交⊙O于F,求EF的长.
(3)设点P(m,n)为⊙O上的任意一点,当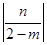 的值最大时,求此时直线BP
的值最大时,求此时直线BP
相应的函数表达式.
(本题10分)如图,已知等边ΔABC,以AB为直径的半圆与BC边交于点D,过点D作⊙O的切线 DF交AC于点F,过点D作DE⊥AB,垂足为点E,过点F作FG⊥AB,垂足为点G,连结GD.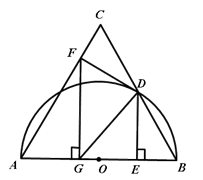
(1)求证:DF⊥AC;
(2)若AB=8,求tan∠FGD的值.
(黄石)父亲节快到了,明明准备为爸爸煮四个大汤圆作早点:一个芝麻馅,一个水果馅,两个花生馅,四个汤圆除内部馅料不同外,其它一切均相同.
(1)求爸爸吃前两个汤圆刚好都是花生馅的概率;
(2)若给爸爸再增加一个花生馅的汤圆,则爸爸吃前两个汤圆都是花生的可能性是否会增大?请说明理由.
如图,在水平地面上竖立着一面墙AB,墙外有一盏路灯D.光线DC恰好通过墙的最高点B,且与地面形成37°角.墙在灯光下的影子为线段AC,并测得AC=5.5米.
(1)求墙AB的高度(结果精确到0.1米);(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80)
(2)如果要缩短影子AC的长度,同时不能改变墙的高度和位置,请你写出两种不同的方法.
若正比例函数y=k1x的图象与反比例函数y=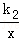 的图象有一个交点坐标是(﹣2,4)
的图象有一个交点坐标是(﹣2,4)
(1)求这两个函数的表达式;
(2)求这两个函数图象的另一个交点坐标.
如图,某建筑物BC上有一旗杆AB,小明在F处,由E点观察到旗杆顶部A的仰角为 ,底部B的仰角为
,底部B的仰角为 ,小明的观测点与地面距离EF为1.6m,
,小明的观测点与地面距离EF为1.6m,
(1)若F与BC相距12m,求建筑物BC的高度;
(2)若旗杆AB长3.15m,求建筑物BC的高度.(结果精确到0.1m)
(参考数据: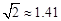 4
4 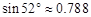 ,
,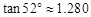 ).
).
(本题14分)在平面直角坐标系中,O为原点,四边形OABC的顶点A在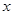 轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点。
轴的正半轴上,OA=4,OC=2,点P,点Q分别是边BC,边AB上的点,连结AC,PQ,点B1是点B关于PQ的对称点。
(1)若四边形OABC为矩形,如图1,
①求点B的坐标;
②若BQ:BP=1:2,且点B1落在OA上,求点B1的坐标;
(2)若四边形OABC为平行四边形,如图2,且OC⊥AC,过点B1作B1F∥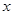 轴,与对角线AC、边OC分别交于点E、点F。若B1E: B1F=1:3,点B1的横坐标为
轴,与对角线AC、边OC分别交于点E、点F。若B1E: B1F=1:3,点B1的横坐标为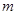 ,求点B1的纵坐标,并直接写出
,求点B1的纵坐标,并直接写出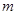 的取值范围。
的取值范围。
如图,在△ABC中,AB=5,AC=9,S△ABC=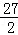 ,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.
,动点P从A点出发,沿射线AB方向以每秒5个单位的速度运动,动点Q从C点出发,以相同的速度在线段AC上由C向A运动,当Q点运动到A点时,P、Q两点同时停止运动,以PQ为边作正方形PQEF(P、Q、E、F按逆时针排序),以CQ为边在AC上方作正方形QCGH.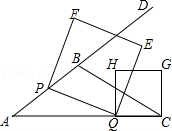
(1)求tanA的值;
(2)设点P运动时间为t,正方形PQEF的面积为S,请探究S是否存在最小值?若存在,求出这个最小值,若不存在,请说明理由;
(3)当t为何值时,正方形PQEF的某个顶点(Q点除外)落在正方形QCGH的边上,请直接写出t的值.
(本小题满分9分)如图,抛物线y=﹣x2+bx+c与x轴交于点A(1,0),B(-5,0)两点,直线y=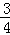 x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是x轴上方的抛物线上一动点,过点P作PF⊥x轴于点F,交直线CD于点E.设点P的横坐标为m.
(1)求抛物线的解析式;
(2)若PE=5EF,求m的值;
(3)若点E′是点E关于直线PC的对称点,是否存在点P,使点E′落在y轴上?若存在,请直接写出相应的点P的坐标;若不存在,请说明理由.
(本小题满分9分)如图,点A(3,2)和点M(m,n)都在反比例函数 的图像上.
的图像上.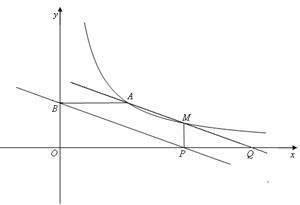
(1)求k的值,并求当m=4时,直线AM的解析式;
(2)过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,直线AM交x轴于点Q,试说明四边形ABPQ是平行四边形.
(3)在(2)的条件下,四边形ABPQ能否是菱形?若能,请求出m的值,若不能,请说明理由.
(本题8分)如图,在□ABCD中, 、
、 是
是 、
、 的中点,
的中点, 、
、 的延长线分别交
的延长线分别交 、
、 的延长线于
的延长线于 、
、 ;
;
(1)求证:BH=AB;
(2)若四边形 为菱形,试判断
为菱形,试判断 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.
某体育用品商店为了解8月份的销售情况,对本月各类商品的销售情况进行调查,并将调查的结果绘制成如下的两幅不完整的统计图.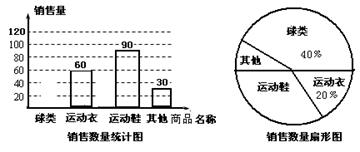
(1)请根据图中提供的信息,将条形图补充完整;
(2)该商店准备按8月份球类商品销量的数量购进球类商品,含篮球、足球、排球三种
球,预计恰好用完货款共3600元.设购进篮球x个,足球y个,三种球的进价和售
价如下表:
| 类别 |
篮球 |
足球 |
排球 |
| 进价(单位:元/个) |
50 |
30 |
20 |
| 预售价(单位:元/个) |
70 |
45 |
25 |
求出y与x之间的函数关系式;
(3)在(2)中的进价和售价的条件下,据实际情况,预计足球销售超过60个后,这种
球就会产生滞销,①假设所购进篮球、足球、排球能全部售出,求出预估利润P(元)与x(个)的函数关系式;②求出预估利润的最大值,并写出此时购进三种球各多少个?