江西省中考模拟数学试卷

已知∠α＝31°，求∠α的补角为（    ）

小林家今年1﹣5月份的用电量情况如图所示，由图可知，相邻两个月中，用电量变化最大的是（   ）

用两块完全相同的长方体搭成如图所示的几何体，这个几何体的主视图是（   ）

在共有23人参加的“安全教育知识”竞赛中，参赛选手要想知道自己是否能进入前12名，只需要了解自己的成绩以及全部成绩的（     ）

现有1角、5角硬币各10枚，从中取出16枚，共计4元，问1角、5角硬币各取多少枚？设1角、5角硬币各取x枚、y枚，可列方程 （    ）   

A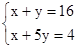．	B．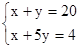
C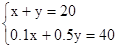．	D．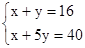

下列选项中，可以用来证明命题“若＞1，则a＞2”是假命题的反例是（   ）

4的算术平方根是       ．

已知一粒米的质量是0.000021千克，这个数字用科学记数法表示为            千克．

如图，数轴上的点P表示的数是－，将点P向右移动3个单位长度得到点P′，则点P′表示的数是          ．

一副三角板如图所示叠放在一起，则图中∠的度数是      度．

请写出一个无实数根的一元二次方程          ．

两棵树植在倾角为24°36′的斜坡上，它们的坡面距离是4米，则它们之间的水平距离是        米（可用计算器，精确到0.1米）．

如图，反比例函数（x＞0）图象上有一点P，PA⊥x轴于A，点B在y轴的正半轴上，△PAB的面积是3，则k =        ．

如图，已知A（-3，0）、B（0，3），半径为1的⊙P在射线AB上运动，那么当⊙P与坐标轴相切时，圆心P的坐标是                 ．

解不等式组，并把解集在数轴上表示出来．

已知方程的解为x=2，先化简，再求它的值．

已知下面是3个5×5的正方形网格，小正方形边长都为1，A、B两点在小网格的顶点上，位置如图所示．现请你分别在三个网格中各画一个△ABC．要求：

（1）顶点C在网格的顶点上；
（2）工具只用无刻度的直尺；
（3）所画的3个三角形互不全等，但面积都为2.

在一个木箱中装有卡片共50张，这些卡片共有三种，它们分别标有1、2、3的字样，除此之外其他都相同，其中标有数字2卡片的张数是标有数字3卡片的张数的3倍少8张．已知从箱子中随机摸出一张标有数字1卡片的概率是．
（1）求木箱中装有标1的卡片张数；
（2）求从箱子中随机摸出一张标有数字3的卡片的概率．

如图，在对Rt△ABC依次进行轴对称（对称轴为y轴）、一次平移和以O位似中心在同侧缩小为原来的一半的变换后得到△OA′B′．

（1）在坐标系中分别画出轴对称、平移变换后相应的二个图形；
（2）设P（a，b）为△ABC边上任意一点，依次分别写出这三次变换后点 P 对应点的坐标．

如图，将△ABC绕点C旋转180°得到△DEC，过点B作AD的平行线，与ED的延长
线交于点F．

（1）求证：D是EF的中点；
（2）连接BD，当△ABC满足什么条件时，BD⊥EF？并说明其理由．

某体育用品商店为了解8月份的销售情况，对本月各类商品的销售情况进行调查，并将调查的结果绘制成如下的两幅不完整的统计图．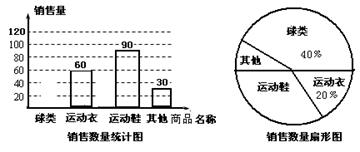

（1）请根据图中提供的信息，将条形图补充完整；
（2）该商店准备按8月份球类商品销量的数量购进球类商品，含篮球、足球、排球三种
球，预计恰好用完货款共3600元.设购进篮球x个，足球y个，三种球的进价和售
价如下表：

 
求出y与x之间的函数关系式；
（3）在（2）中的进价和售价的条件下，据实际情况，预计足球销售超过60个后，这种
球就会产生滞销，①假设所购进篮球、足球、排球能全部售出，求出预估利润P（元）与x（个）的函数关系式；②求出预估利润的最大值，并写出此时购进三种球各多少个？

如图2，边长为2的等边△ABC内接于⊙O，△ABC绕圆心O顺时针方向旋转得到△，A′C′分别与AB、AC交于E、D点，设旋转角度为．

（1）当＝     ，△A′B′C′与△ABC出现旋转过程中的第一次完全重合；
（2）当＝60°时（如图1），该图（     ）
A．是中心对称图形但不是轴对称图形   
B．是轴对称图形但不是中心对称图形
C．既是轴对称图形又是中心对称图形  
D．既不是轴对称图形也不是中心对称图形 
（3）如图2，当，△ADE的周长是否会发生变化，如会变化，说明理由，如不会变化，求出它的周长.

已知抛物线L₁：和抛物线L₂：，其中，抛物线L₂与x轴相交于A、B两点，其图像如图所示．
（1）下列说法你认为正确的序号是                   ；
①抛物线L₁和L₂与轴交于同一点F；  ② 抛物线L₁和L₂开口都向上；
③抛物线L₁和L₂的对称轴是同一条直线；      ④ A （-5，0）， B（-1，0）
（2）抛物线L₁和L₂相交于点E、F，当的值发生变化时，请判断线段EF的长度是否发生变化，并说明理由；
（3）在（2）中，若抛物线L₁的顶点为M，抛物线L₂的顶点为N. 问是否存在实数，使MN＝2EF，如存在，求出实数，如不存在，请说明理由.

如图，已知正方形ABCD的边长为4，E是射线CB上的一个动点，过点D作DF⊥DE，交BA的延长线于点F，EF交对角线AC所在的直线于点M，DE交AC于点N ．

（1）求证：CE=AF；
（2）设CE=x，△AMF的面积为y，求y与x之间的函数关系式，并写出自变量x的取值范围；
（3）随着点E在射线CB上运动，NA·MC的值是否会发生变化？若不变，请求出NA·MC的值；若变化，请说明理由．