高中物理计算题

一传送带装置如图所示，其中AB段是水平的，长度L_AB＝4 m，BC段是倾斜的，长度L_BC＝5 m，倾角为θ＝37°，AB和BC由B点通过一段短的圆弧连接(图中未画出圆弧)，传送带以v＝4 m/s的恒定速率顺时针运转，已知工件与传送带间的动摩擦因数μ＝0.5，重力加速度g取10 m/s².现将一个工件(可看做质点)无初速度地放在A点，求：

(1)工件第一次到达B点所用的时间；
(2)工件沿传送带上升的最大高度；
(3)工件运动了23 s后所在的位置．

一飞船在某星球表面附近，受星球引力作用而绕其做匀速圆周运动的速率为v₁，飞船在离该星球表面高度为h处，受星球引力作用而绕其做匀速圆周运动的速率为v₂，已知万有引力常量为G.试求：
(1)该星球的质量；
(2)若设该星球的质量为M，一个质量为m的物体在离该星球球心r远处具有的引力势能为E_p＝－，则一颗质量为m₁的卫星由r₁轨道变为r₂(r₁＜r₂)轨道，对卫星至少做多少功？(卫星在r₁、r₂轨道上均做匀速圆周运动，结果请用M、m₁、r₁、r₂、G表示)

山地滑雪是人们喜爱的一项运动，一滑雪道ABC的底部是一半径为R的圆，圆与雪道相切于C点，C点的切线水平，C点与水平雪地间距离为H，如图所示，D是圆的最高点，一运动员从A点由静止下滑，刚好能经过圆轨道最高点D旋转一周，再经C后被水平抛出，当抛出时间为t时，迎面水平刮来一股强风，最终运动员以速度v落到了雪地上，已知运动员连同滑雪装备的总质量为m，重力加速度为g，不计遭遇强风前的空气阻力和雪道及圆轨道的摩擦阻力，求：

(1)A、C的高度差为多少时，运动员刚好能过D点？
(2)运动员刚遭遇强风时的速度大小及距地面的高度；
(3)强风对运动员所做的功．

(1)研究发现两个氘核(H)可聚变成He，已知氘核的质量为2.013 6 u，中子的质量为1.008 7 u， He核质量为3.015 0 u．若质量亏损1 u对应的核能为931.5 MeV，则两个氘核聚变成He核的核反应方程为________________；上述反应中释放的核能为________．
(2)如图所示，光滑水平面上三个物块A、B、C，A、B间有压缩且被锁定的轻弹簧，三物块均处于静止状态．现解除对弹簧的锁定，B离开弹簧后，以速度v₀与C相碰，最终B与A运动的速度相同，已知m_A＝6 kg，m_B＝1 kg，m_C＝14 kg，求B与C相碰后C的速度大小．

(1)我国科学家经过艰苦努力，率先建成了世界上第一个全超导托克马克试验装置并调试成功．这种装置被称为“人造太阳”，它能够承受上亿摄氏度高温且能够控制等离子态的核子发生聚变并稳定持续地输出能量，就像太阳一样为人类提供无限清洁能源．在该装置内发生的核反应方程是H＋H―→He＋X，其中粒子X的符号是________．已知H的质量是m₁， H的质量是m₂，He的质量是m₃，X的质量是m₄，光速是c，则发生一次上述聚变反应所释放的核能表达式为___________________________________________．
(2)光滑水平面上静止放置一长方形木板B，B的质量为M＝2 kg，B的右端离竖直墙6 m．现有一小物体A，其质量m＝1 kg，以v₀＝6 m/s的速度从B的左端水平滑上B，如图所示．A和B之间的动摩擦因数μ＝0.4，B与墙碰撞时间极短，且碰撞时无能量损失．要使A最终不脱离B，B的最短长度是多少？

(1)2011年中国宣布突破快中子增殖反应堆技术，使核反应原料利用率提升到百分之六十以上．第一代核反应堆以铀235为裂变燃料，而在天然铀中占99%的铀238不能被利用，为了解决这个问题，科学家们研究出快中子增殖反应堆，使铀238变成高效核燃料．在快中子增殖反应堆中，使用的核燃料是钚239，裂变时释放出快中子，周围的铀238(U)吸收快中子后变成铀239(U)，铀239很不稳定，经过________次β衰变后变成钚239(Pu)，从而实现核燃料的增殖．铀238转变为钚239的全过程的核反应方程式为____________________________________________.
(2)如图所示，长为L＝2 m的木板A质量为M＝2 kg，A静止于足够长的光滑水平面上，小物块B(可视为质点)静止于A的左端，B的质量为m₁＝1 kg，曲面与水平面相切于M点．现让另一小物块C(可视为质点)从光滑曲面上离水平面高h＝3.6 m处由静止滑下，C与A相碰后与A粘在一起，C的质量为m₂＝1 kg，A与C相碰后，经一段时间B可刚好离开A，g＝10 m/s².求A、B之间的动摩擦因数μ.

(1)有频率相同、振动方向相同的两个声源S₁和S₂，如图所示．一人站在声源北方的A点，此人此时听到的声音很响，这个人向东慢慢移动，声音逐渐减弱，到B点时几乎听不到声音，测得A、B间距离为1.5 m．则：

①S₁、S₂声波的波长λ为多少？
②若此人由B点再向正南方向移动，声音逐渐变响，那么，此人沿正南方向至少走多远，声音又变得很响？
(2)如图所示，玻璃棱镜ABCD可以看成是由ADE、ABE、BCD三个直角三棱镜组成．一束频率为5.3×10¹⁴ Hz的单色细光束从AD面入射，在棱镜中的折射光线如图中ab所示，ab与AD面的夹角α＝60°.已知光在真空中的传播速度c＝3×10⁸ m/s，玻璃的折射率n＝1.5，求：

①该束入射光线的入射角；
②该束光线第一次从玻璃棱镜中出射时的折射角．(结果可用三角函数表示)

如图所示，两根竖直放置在绝缘面上的金属框架．框架的上端接有电容为C的电容器．框架上有一质量为m、长为l的金属棒，平行于地面放置，与框架接触良好无摩擦，棒离桌面高度为h.磁感应强度为B的匀强磁场与框架平面相垂直，开始时电容器不带电．自静止起将棒释放，求棒从释放到落到地面所需要的时间？

放在水平地面上的一物块，受到方向不变的水平推力F的作用，力F的大小与时间t的关系和物块速度v与时间t的关系如图所示．重力加速度g＝10 m/s².求：

(1)物块在运动过程中受到的滑动摩擦力大小；
(2)物块在3～6 s中的加速度大小；
(3)物块与地面间的动摩擦因数．

如图（a）所示，木板OA可绕轴O在竖直平面内转动， 某研究小组利用此装置探索物块在方向始终平行于斜面、大小为F＝8N的力作用下加速度与斜面倾角的关系。已知物块的质量m＝1kg，通过DIS实验，得到 如图（b）所示的加速度与斜面倾角的关系图线。若物块与木板间的动摩擦因数为0.2，假定物块与木板间的最大静摩擦力始终等于滑动摩擦力，g取10m/s²。试问：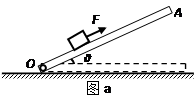

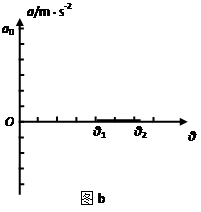
（1）图（b）中图线与纵坐标交点a_o多大？
（2）图（b）中图线与θ轴交点坐标分别为θ₁和θ₂，木板处于该两个角度时的摩擦力指向何方？说明在斜面倾角处于θ₁和θ₂之间时物块的运动状态。
（3）如果木板长L＝2m，倾角为37°，物块在F的作用下由O点开始运动，为保证物块不冲出木板顶端，力F最多作用多长时间？（取sin37°＝0.6，cos37°＝0.8）

如图所示，在竖直平面内有一水平向右的匀强电场，场强E＝1.0×10⁴ N/C.电场内有一半径R＝2.0 m的光滑绝缘细圆环形轨道竖直放置且固定，有一质量为m＝0.4 kg、带电荷量为q＝＋3.0×10^－4 C的带孔小球穿过细圆环形轨道静止在位置A，现对小球沿切线方向作用一瞬时速度v_A，使小球恰好能在光滑绝缘细圆环形轨道上做圆周运动，取圆环的最低点为重力势能和电势能的零势能点．已知g＝10 m/s²，sin 37°＝0.6，cos 37°＝0.8，求：

(1)瞬时速度v_A的大小；
(2)小球机械能的最小值．

如图所示，光滑水平桌面上有一质量为m的物块，桌面右下方有半径为R的光滑圆弧形轨道，圆弧所对应的圆心角为2θ，轨道左右两端点A、B等高，左端A与桌面的右端的高度差为H.已知物块在一向右的水平拉力作用下沿桌面由静止滑动，撤去拉力后物块离开桌面，落到轨道左端时其速度方向与轨道相切，随后沿轨道滑动，若轨道始终与地面保持静止(重力加速度为g)．

求：(1)拉力对物块做的功；
(2)物块滑到轨道最低点时受到的支持力大小．

如图所示，有一长为L的细线，细线的一端固定在O点，另一端拴一质量为m的小球，现使小球恰好在竖直平面内做完整的圆周运动，已知水平面上的C点在O点的正下方，且到O点的距离为1.9 L，不计空气阻力，求：(g＝10 m/s²)

(1)小球通过最高点A的速度v_A；
(2)若小球通过最低点B时，细线对小球的拉力T恰好为小球重力的6倍，且小球通过B点时细线断裂，求小球落地点到C的距离．

如图所示，aa′、bb′、cc′、dd′为区域Ⅰ、Ⅱ、Ⅲ的竖直边界，三个区域的宽度相同，长度足够大，区域Ⅰ、Ⅲ内分别存在垂直纸面向外和向里的匀强磁场，区域Ⅱ存在竖直向下的匀强电场．一群速率不同的带正电的某种粒子，从边界aa′上的O处，沿着与Oa成30°角的方向射入Ⅰ区．速率小于某一值的粒子在Ⅰ区内运动时间均为t₀；速率为v₀的粒子在Ⅰ区运动后进入Ⅱ区．已知Ⅰ区的磁感应强度的大小为B，Ⅱ区的电场强度大小为2Bv₀，不计粒子重力．求：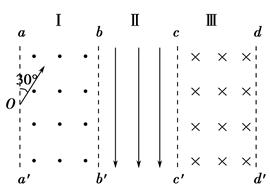

(1)该种粒子的比荷；
(2)区域Ⅰ的宽度d；
(3)速率为v₀的粒子在Ⅱ区内运动的初、末位置间的电势差U；
(4)要使速率为v₀的粒子进入Ⅲ区后能返回到Ⅰ区，Ⅲ区的磁感应强度B′的大小范围应为多少？

(16分)如图所示，在平面直角坐标系xoy中的第一 象限内存在磁感应强度大小为B、方向垂直于坐标平面向里的有界圆形匀强磁场区域(图中未画出)；在第二象限内存在沿x轴负方向的匀强电场．一粒子源固定在 x轴上坐标为(－L，0)的A点．粒子源沿y轴正方向释放出速度大小为v的电子，电子恰好能通过y轴上坐标为(0，2L)的C点，电子经过磁场偏转后恰好 垂直通过第一象限内与x轴正方向成15°角的射线ON(已知电子的质量为m，电荷量为e，不考虑粒子的重力和粒子之间的相互作用)．求：

⑴匀强电场的电场强度E的大小；
⑵电子离开电场时的速度方向与y轴正方向的夹角θ；
⑶圆形磁场的最小半径R_min．