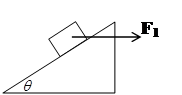
质量为m=1kg的物体放在倾角θ=45°的固定斜面上,设物体与斜面间的动摩擦因数为µ=0.2,一个沿水平方向推力F1使物体匀速上滑,如图所示求F1的大小。(g=10m/s2)
重为40 N的物体与竖直墙面间的动摩擦因数为μ = 0.4,若用斜向上与水平方向成370的推力F =" 50" N支撑住物体,物体处于静止状态,如图所示。这时物体受到的摩擦力是多少牛?要使物体匀速下滑,推力的方向不变,则大小应变为多大?(sin 37° = 0.6,cos 37° = 0.8)
如图所示,用一根绳子a把物体挂起来,再用另一根水平的绳子b 把物体拉向一旁固定起来。 物体的重力是80 N,绳子a与竖直方向的夹角θ = 37°,绳子a与b对物体的拉力分别是 多大?(sin 37° = 0.6,cos 37° = 0.8)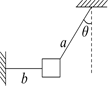
如图所示,质量均为m的A、B两球,以轻质弹簧连接后置于光滑水平面上,开始弹簧处于自然状态。一质量为 的泥丸P以水平速度v0沿A、B连线向A运动,击中A并粘合在一起,求以后的运动过程中弹簧的最大弹性势能。
的泥丸P以水平速度v0沿A、B连线向A运动,击中A并粘合在一起,求以后的运动过程中弹簧的最大弹性势能。
如图所示,三棱镜的横截面为直角三角形ABC,∠A=30°,∠B=60°,一束平行于AC的光线自AB边的P点射入三棱镜,若棱镜的折射率n=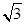 ,光在真空中的速度为c。
,光在真空中的速度为c。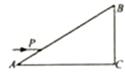
(1)求光在棱镜中的传播速度;
(2)通过计算说明光线射出棱镜时的出射方向。
如图,一固定的竖直汽缸由一大一小两个同轴圆筒组成,两圆筒中各有一个活塞,已知大活塞的质量为m1=2.50kg,横截面积为S1=80.0cm2,小活塞的质量为m2=1.50kg,横截面积为S2=40.0cm2,两活塞用刚性轻杆连接,间距保持为l=40.0cm,汽缸外大气的压强为p=1.00×105Pa,温度为T=303K,初始时大活塞与大圆筒底部相距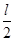 ,两活塞间封闭气体的温度为T1=495K。现汽缸内气体温度缓慢下降,活塞缓慢下移,忽略两活塞与汽缸壁之间的摩擦,重力加速度大小g取10m/s2,求:
,两活塞间封闭气体的温度为T1=495K。现汽缸内气体温度缓慢下降,活塞缓慢下移,忽略两活塞与汽缸壁之间的摩擦,重力加速度大小g取10m/s2,求:
(1)在大活塞与大圆筒底部接触前的瞬间,缸内封闭气体的温度;
(2)缸内封闭的气体与缸外大气达到热平衡时,缸内封闭气体的压强。
同学们参照伽利略时期演示平抛运动的方法制作了如图所示的实验装置。图中水平放置的底板上竖直地固定有M板和N板。M板上部有一半径为R的 圆弧形的粗糙轨道,P为最高点,Q为最低点,Q点处的切线水平,距底板高为
圆弧形的粗糙轨道,P为最高点,Q为最低点,Q点处的切线水平,距底板高为 。N板上固定有三个圆环。将质量为
。N板上固定有三个圆环。将质量为 的小球从P处静止释放,小球运动至Q飞出后无阻碍地通过各圆环中心,落到底板上距Q水平距离为L处。不考虑空气阻力,重力加速度为g。求:
的小球从P处静止释放,小球运动至Q飞出后无阻碍地通过各圆环中心,落到底板上距Q水平距离为L处。不考虑空气阻力,重力加速度为g。求:
(1)距Q水平距离为 的圆环中心到底板的高度;
的圆环中心到底板的高度;
(2)小球运动到Q点时速度的大小以及对轨道压力的大小和方向;
(3)摩擦力对小球做的功。
如图,一长为10cm的金属棒用两个完全相同的弹簧水平地悬挂在匀强磁场中,磁场的磁感应强度大小为0.1T,方向垂直于纸面向里,弹簧上端固定,下端与金属棒绝缘,金属棒通过开关与一电动势为12V的电池相连,电路总电阻为2Ω,已知开关断开时两弹簧的伸长量均为0.5cm。闭合开关,系统重新平衡后,两弹簧的伸长量与开关断开时相比均改变了0.3cm,重力加速度大小取10m/s2,判断开关闭合后金属棒所受安培力的方向,并求出金属棒的质量。
如图所示,质量为m的由绝缘材料制成的球与质量为M=19m的金属球并排悬挂,摆长相同,均为l。现将绝缘球拉至与竖直方向成θ=60°的位置自由释放,摆至最低点与金属球发生弹性碰撞。在平衡位置附近存在垂直于纸面的磁场,已知由于磁场的阻尼作用,金属球总能在下一次碰撞前停在最低点处,重力加速度为g。求:
(1)第一次碰撞前绝缘球的速度v0;
(2)第一次碰撞后绝缘球的速度v1;
(3)经过几次碰撞后绝缘球偏离竖直方向的最大角度将小于37°。(你可能用到的数学知识:sin37°=0.6,cos37°=0.8,0.812=0.656,0.813=0.531,0.814=0.430,0.815=0.349,0.816=0.282)
如图所示,MNPQ是一块截面为正方形的玻璃砖,其边长MN=30 cm。一束激光AB射到玻璃砖的MQ面上(入射点为B)进入玻璃砖后在QP面上的F点(图中未画出)发生全反射,恰沿DC方向射出。其中B为MQ的中点,∠ABM=30°,PD="7.5" cm,∠CDN=30°。
①画出激光束在玻璃砖内的光路示意图,求出QP面上的反射点F到Q点的距离QF;
②求出该玻璃砖的折射率;
③求出激光束在玻璃砖内的传播速度(真空中光速c=3×108m/s)。
图为一注射器,针筒上所标刻度是注射器的容积,最大刻度Vm=20ml,其活塞的横截面积为2cm2。先将注射器活塞移到刻度V1=18ml的位置,然后用橡胶帽密封住注射器的针孔。已知环境温度t1=27℃,大气压p0=1.0×105Pa,为使活塞移到最大刻度处,试问:(活塞质量及活塞与针筒内壁间的摩擦均忽略不计。)
(i)若把注射器浸入水中缓慢加热,水温须升至多少℃?
(ii)若沿注射器轴线用力向外缓慢拉活塞,拉力须达到多大?
如图所示,有同学做实验时不慎将圆柱形试管塞卡于试管底部,该试管塞中轴穿孔。为了拿出试管塞而不损坏试管,该同学紧握试管让其倒立由静开始竖直向下做匀加速直线运动,t=0.20s后立即停止,此时试管下降H=0.80m,试管塞将恰好能从试管口滑出。已知试管总长l=21.0cm,底部球冠的高度h=1.0cm,试管塞的长度为d=2.0cm,设试管塞相对试管壁滑动时受到的的摩擦力恒定,不计空气阻力,重力加速度g=l0m/s2。求: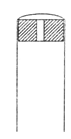
(1)试管塞从静止开始到离开试管口的总位移;
(2)试管塞受到的滑动摩擦力与其重力的比值。
空间有一匀强电场,电场方向与纸面平行。一带正电、电量为q,质量为m的小球(重力不计),在恒定拉力F的作用下沿虚线以速度 由M匀速运动到N,如图所示。已知力F和MN间夹角为
由M匀速运动到N,如图所示。已知力F和MN间夹角为 ,MN间距离为L,则:
,MN间距离为L,则:
(1)匀强电场的电场强度大小为多少?
(2)MN两点的电势差为多少?
(3)当带电小球到达N点时,撤去外力F,则小球回到过M点的等势面时的动能为多少?
如图所示,两块平行极板AB、CD正对放置,极板CD的正中央有一小孔,两极板间距离AD为d,板长AB为2d,两极板间电势差为U,在ABCD构成的矩形区域内存在匀强电场,电场方向水平向右。在ABCD矩形区域以外有垂直于纸面向里的范围足够大的匀强磁场。极板厚度不计,电场、磁场的交界处为理想边界。将一个质量为m、电荷量为+q的带电粒子在极板AB的正中央O点,由静止释放。不计带电粒子所受重力。
(1)求带电粒子经过电场加速后,从极板CD正中央小孔射出时的速度大小;
(2)为了使带电粒子能够再次进入匀强电场,且进入电场时的速度方向与电场方向垂直,求磁场的磁感应强度的大小,并画出粒子运动轨迹的示意图。
(3)通过分析说明带电粒子第二次离开电场时的位置,并求出带电粒子从O点开始运动到第二次离开电场区域所经历的总时间。