高中物理计算题

如图所示，细绳一端系着质量为M=1.0kg的物体,静止在水平板上，另一端通过光滑小孔吊着质量m=0.3kg的物体，M的中点与圆孔距离为L=0.2m，并知M与水平面的最大静摩擦力为2N，现使此平面绕中心轴线以角速度ω转动，为使m处于静止状态。角速度ω取值范围? (g＝10m/s²)

将一物体以10m/s的速度从20m高度水平抛出，（g取10m/s²）求：
（1）物体经多长时间落地？
（2）物体从抛出到落地，水平方向移动的距离多大？
（3）物体落地时速度的大小。

质量为25kg的小孩坐在秋千板上，小孩离系绳子的横梁4m。如果秋千板摆到最低点时，小孩运动速度的大小是4m/s，她对秋千板的压力是多大？（g取10m/s²）

无风时气球匀速竖直上升的速度是4m/s，现自西向东的风速大小为3m/s，则气球相对地面运动的速度大小为多少?

如图所示，两个质量均为m=1kg的物块A、B套在水平粗糙的CD杆上，并用不可伸长的轻绳连接，整个装置能绕过CD中点的轴OO₁转动，物块A、B与杆CD间的动摩擦因素μ=0.2，开始时绳子处于自然长度（绳子恰好伸直但无弹力），物块A到OO₁轴的距离为r=0.1m，物块B到OO₁轴的距离为2r，现让该装置从静止开始转动，使转速ω逐渐增大，但A、B相对于杆一直未滑动，最大静摩擦力可看做等于滑动摩擦力，g=10m/s²，试求：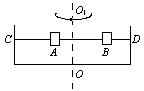

（1）当转速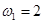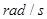时，杆对B的摩擦力？
（2）轻绳中刚要产生张力时，转速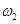等于多少？
（3）当转速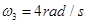时，杆对A的摩擦力？

为纪念“光纤之父”、诺贝尔物理学奖获得者高锟的杰出贡献，早在1996年中国科学院紫金山天 文台就将一颗于1981年12月3日发现的国际编号为“3463”的小行星命名为“高锟星”。已知“高锟星”半径为R，其表面的重力加速度为g，万有引力常量为G，在不考虑自转的情况，求解以下问题：（以下结果均用字母表达即可）
（1）假设“高锟星”为一均匀球体，试求“高锟星”的平均密度；（球体积）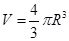
（2）卫星环绕“高锟星”运行的第一宇宙速度；
（3）假设某卫星绕“高锟星”做匀速圆周运动且运行周期为T，求该卫星距地面的高度。

如图所示，两绳系一质量为0.1 kg的小球，两绳的另一端分别 固定于轴的A、B两处，上面绳长2 m，两绳拉直时与轴的夹角分别为30°和45°，问球的角速度在什么范围 内两绳始终有张力？（g取10 m/s²）

如图位于竖直平面上半径为R 的1/4光滑圆弧轨道AB，A点距离地面高度为H，质量为m的小球从A点由静止释放，通过B点时对轨道的压力为3 mg，最后落在地面C处，不计空气阻力，求：

（1）小球通过B点时向心力的大小 ；
（2）小球通过B点时速度的大小；
（3）小球落地点C与B点的水平距离。

在远距离输电时，要考虑尽量减少输电线上的功率损失。有一个小型发电站，发电机输出的电功率为P=500kW，当使用U=5kV的电压输电时，测得安装在输电线路起点和终点处的两只电度表一昼夜示数相差4800 kWh。求：
（1）输电线上的电流 I、输电线的总电阻r和输电线上的损耗的电压U_损
（2）若想把损耗功率控制在输送功率的1.6%，又不改变输电线，那么电站应使用多高的电压向外输电？线路损耗的电压是多少？

如图，一固定的斜面，其倾角为θ=30º，另一边与水平地面垂直，顶端有一定滑轮，跨过定滑轮的细线两端分别与物块A、B相连，A的质量为4m，B的质量为m。开始时，将B按在地上不动，然后放手，让A沿斜面下滑而B上升，所有摩擦均忽略不计。当A下滑距离为S时，细线突然断了。求B上升的最大高度。（设B不会与定滑轮相碰）

如图所示，斜面足够长，其倾角为α，质量为m的滑块，距挡板P为s₀，以初速度v₀沿斜面上滑，滑块与斜面间的动摩擦因数为μ，滑块所受摩擦力小于滑块沿斜面方向的重力分力，若滑块每次与挡板相碰均无机械能损失(即速度大小不变方向相反)，求滑块在斜面上经过的总路程为多少？

如图所示是伦敦奥运会期间水上运动中心安置在游泳池底部的照相机拍摄的一张照片，相机的镜头竖直向上．照片中，水立方运动馆的景象呈现在半径的圆形范围内，水面上的运动员手到脚的长度.若已知水的折射率，运动员的实际身高，请计算该游泳池的水深H。

人们利用发电机把天然存在的各种形式的能(水能、风能、煤燃烧的化学能等)转化为电能，为了合理地利用这些能源，发电站要修建在靠近这些天然资源的地方，但是用电的地方往往很远，因此，就需要高压输送线路把电能输送到远方。如果某发电站将的电压直接地加在高压输送线路的输入端，向远方供电，且输送的电功率为。则此时安装在高压输送线路的入端和终端的电能表一昼夜读数就相差 (1＝1度电)。求：
（1）此种情况下，高压线路的终端功率和输电效率．
（2）若要使此高压输电线路的输电效率为97%，则在发电站处应安装一个变压比是多少的变压器？

足够长光滑斜面BC的倾角α＝53º，小物块与水平面间的动摩擦因数为0.5，水平面与斜面之间B点有一小段弧形连接，一质量m=2kg的小物块静止于A点。现在AB段对小物块施加与水平方向成α＝53º的恒力F作用，如图（a）所示，小物块在AB段运动的速度－时间图像如图（b）所示，到达B点迅速撤去恒力F。（已知sin53º＝0.8，cos53º＝0.6）。求：

（1）小物块所受到的恒力F；
（2）小物块从B点沿斜面向上运动，到返回B点所用的时间；
（3）小物块能否返回到A点？若能，计算小物块通过A点时的速度；若不能，计算小物块停止运动时离B点的距离。

有一个导热性能良好的圆柱形容器，顶部由一活塞密封，容器内盛有一定量的水，通过一根细管（体积可忽略）与外界相通，如图所示。当温度为t℃时，细管中水面与容器中水面相平，被封闭空气柱的高度为H，此时水面距细管顶端出口处高度差为h。已知大气压强为P₀，水的密度为ρ，重力加速度为g。

（1）若用力压活塞，使它缓慢向下移动，整个过程中保持温度不变，要使水从细管顶端流出，活塞移动距离Δh至少多大？
（2）若保持活塞在初位置不动，让温度缓慢升高，要使水从细管顶端流出，则温度至少要升高到多少摄氏度？