如图所示,半径为R的光滑半圆环轨道竖直固定在一水平光滑的桌面上,桌面距水平地面的高度也为R,在桌面上轻质弹簧被a、b两个小球挤压(小球与弹簧不拴接),处于静止状态.同时释放两个小球,小球a、b与弹簧在水平桌面上分离后,a球从B点滑上光滑半圆环轨道并恰能通过半圆环轨道最高点A,b球则从桌面C点滑出后落到水平地面上,落地点距桌子右侧的水平距离为 .已知小球a质量为m,重力加速度为g.求:
.已知小球a质量为m,重力加速度为g.求:
(1)释放后b球离开弹簧时的速度大小.
(2)释放后a球离开弹簧时的速度大小.
(3)小球b的质量.
(4)释放小球前弹簧具有的弹性势能.
某电厂要将电能输送到较远的用户,输送的总功率为9.8×104 W,电厂输出电压仅为350 V,为减少输送功率损失,先用一升压变压器将电压升高再输出.已知输电线路的总电阻为4 Ω,允许损失的功率为输送功率的5%,用户所需电压为220 V,求升压、降压变压器的原、副线圈的匝数比各是多少?
在如图甲所示的电路中,螺线管匝数n = 1500匝,横截面积S = 20cm2。螺线管导线电阻r = 1.0Ω,R1 = 4.0Ω,R2 = 5.0Ω,C=30μF。在一段时间内,穿过螺线管的磁场的磁感应强度B按如图乙所示的规律变化。求:
(1)求螺线管中产生的感应电动势;
(2)闭合S,电路中的电流稳定后,求电阻R1的电功率;
(3)闭合S,电路中的电流稳定后,求电容器所带电量。
如图,质量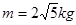 的物体在水平外力的作用下在一水平面上运动,物体和水平面间的动摩擦因数
的物体在水平外力的作用下在一水平面上运动,物体和水平面间的动摩擦因数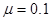 ,已知物体运动过程中的坐标与时间的关系为
,已知物体运动过程中的坐标与时间的关系为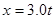 (m),
(m),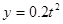 (m),
(m),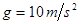 。根据以上条件求:
。根据以上条件求:
(1) 时物体的位置坐标;
时物体的位置坐标;
(2) 时物体的速度大小;
时物体的速度大小;
(3) 时刻水平外力的大小。
时刻水平外力的大小。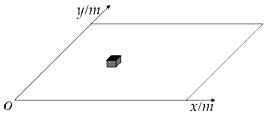
中国现已掌握神舟飞船与太空中目标飞行器的自动和手动对接技术,这就意味着宇航员可乘飞船对在轨航天器进行维护。宇航员现欲乘神舟飞船对在距月球表面高度为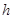 圆轨道上运行的月球卫星进行在轨维修。
圆轨道上运行的月球卫星进行在轨维修。
已知月球半径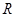 ,月球表面重力加速度为
,月球表面重力加速度为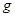 ,计算过程中可不计地球引力的影响,试根据你所学的知识解答下列问题:
,计算过程中可不计地球引力的影响,试根据你所学的知识解答下列问题:
(1)试求维护卫星时航天飞机的速度大小。计算结果用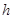 、
、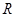 、
、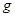 表示。
表示。
(2)已知地球自转周期为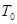 ,则该卫星每天可绕月球转几圈?计算结果用
,则该卫星每天可绕月球转几圈?计算结果用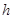 、
、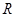 、
、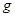 、
、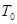 表示。
表示。
一可看作质点滑块从一平台右端以某一速度水平抛出,恰好到右下方倾角为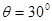 的斜面顶端时速度沿斜面方向并沿斜面运动到斜面底端。已知平台到斜面顶端的竖直高度
的斜面顶端时速度沿斜面方向并沿斜面运动到斜面底端。已知平台到斜面顶端的竖直高度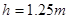 ,斜面与滑块之间的摩擦因数为
,斜面与滑块之间的摩擦因数为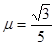 ,斜面顶端底端的竖直高度
,斜面顶端底端的竖直高度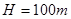 ,
, 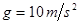 求:
求:
(1)滑块水平抛出的初速度大小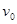
(2)滑块从抛出到斜面底端的时间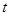
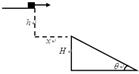
如图所示,摩托车做腾跃特技表演,沿曲面冲上高0.8m顶部水平高台,接着以v=3m/s水平速度离开平台,落至地面时,恰能无碰撞地沿圆弧切线从A点切入光滑竖直圆弧轨道,并沿轨道下滑。A、B为圆弧两端点,其连线水平。已知圆弧半径为R=1.0m,人和车的总质量为180kg,特技表演的全过程中,阻力忽略不计。(计算中取g=10m/s2,sin53°=0.8,cos53°=0.6)。求:
(1)从平台飞出到A点,人和车运动的水平距离s;
(2)从平台飞出到达A点时速度及圆弧对应圆心角θ;
(3)人和车运动到达圆弧轨道A点时对轨道的压力;
(4)人和车运动到圆弧轨道最低点O速度vo= m/s此时对轨道的压力。
m/s此时对轨道的压力。
已知月球质量是地球质量的1/81,月球半径是地球半径的1/3.8.
求:(1)在月球和地球表面附近,以同样的初速度分别竖直上抛一个物体时,上升的最大高度之比是多少?
(2)在距月球和地球表面相同高度处(此高度较小),以同样的初速度分别水平抛出一个物体时,物体的水平射程之比为多少?
半径为R的半圆形轨道固定在水平地面上,一质量为m的小球从最低点A处冲上轨道,当小球从轨道最高点B处水平飞出时,其速度的大小为v= 试求:
试求:
(1)小球在B处受到轨道弹力的大小;
(2)小球落地点到A的距离.
如图所示,A物块以速度v沿竖直杆匀速下滑,经细绳通过定滑轮拉动物块B在水平方向上运动.当细绳与水平面夹角为θ时,求物块B运动的速度大小.
一架农用飞机做水平匀速飞行时,投下一物体,在物体落地前1s时,其速度方向与水平方向夹37°角,落地前瞬间,速度方向与水平方向夹53°角.不计空气阻力,求飞机飞行的高度与速度.
如图所示,波沿x轴正方向传播,质点p的坐标x=0.32 m.从此时刻开始计时.
(1)若每间隔最小时间0.4 s重复出现波形图,求波速.
(2)若p点经0.4 s第一次达到正向最大位移,求波速.
(3)若p点经0.4 s到达平衡位置,求波速.
如图,悬挂在天花板上的长为2L的轻杆可绕光滑的轴O在竖直面内转动,在杆的中点和下端各固定一个质量为m的小球A、B ,把杆从与竖直方向成θ角的初位置释放,求杆转到竖直位置的过程中杆对B球所做的功。
已知一个可视为球体的天体,其自转周期为T,在它的赤道上,用弹簧秤测某一物体的重力是在它两极处测得的重力的0.8倍,已知万有引力常量为G 。求该天体的平均密度ρ是多少?
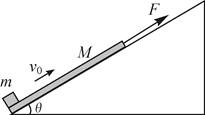
如图所示,质量M=1kg的木板静置于倾角θ=37°、足够长的固定光滑斜面底端。质量m=1kg的小物块(可视为质点)以初速度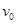 =4m/s从木板的下端冲上木板,同时在木板的上端施加一个沿斜面向上F=3.2N的恒力。若小物块恰好不从木板的上端滑下,求木板的长度
=4m/s从木板的下端冲上木板,同时在木板的上端施加一个沿斜面向上F=3.2N的恒力。若小物块恰好不从木板的上端滑下,求木板的长度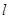 为多少?已知小物块与木板之间的动摩擦因数
为多少?已知小物块与木板之间的动摩擦因数 ,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8。
,重力加速度g=10m/s2,sin37°=0.6,cos37°=0.8。