如图所示装置中,区域Ⅰ中有竖直向上的匀强电场,电场强度为E,区域Ⅱ内有垂直纸面向外的水平匀强磁场,磁感应强度为B。区域Ⅲ中有垂直纸面向里的水平匀强磁场,磁感应强度为2B。一质量为m、带电量为q的带负电粒子(不计重力)从左边界O点正上方的M点以速度v0水平射入电场,经水平分界线OP上的A点与OP成60°角射入Ⅱ区域的磁场,并垂直竖直边界CD进入Ⅲ区域的匀强磁场中。求:
(1)粒子在Ⅱ区域匀强磁场中运动的轨道半径
(2)O、M间的距离
(3)粒子从M点出发到第二次通过CD边界所经历的时间
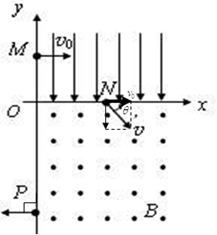
如图所示,直线MN上方存在着垂直纸面向里、磁感应强度为B的匀强磁场,质量为m、电荷量为-q(q>0)的粒子1以速度v1=v0从O点垂直射入磁场,其方向与MN的夹角 =30o;质量为m、电荷量为+q的粒子2以速度
=30o;质量为m、电荷量为+q的粒子2以速度 也从O点垂直射入磁场,其方向与MN的夹角
也从O点垂直射入磁场,其方向与MN的夹角 =60o。已知粒子l、2同时到达磁场边界的A、B两点(图中未画出),不计粒子的重力及粒子间的相互作用。
=60o。已知粒子l、2同时到达磁场边界的A、B两点(图中未画出),不计粒子的重力及粒子间的相互作用。
(1)请画出粒子1和2在磁场中运动的轨迹;
(2)求两粒子在磁场边界上的穿出点A、B之间的距离d;
(3)求两粒子进入磁场的时间间隔 t;
t;
(4)若MN下方有一匀强电场,使两粒子在电场中相遇,其中的粒子1做匀加速直线运动。求电场强度E的大小。
(10分)如图所示,比荷为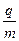 的负离子,以速度v垂直磁感应强度为B的匀强磁场由.P点进入,界面I和Ⅱ平行,宽度为L(L<
的负离子,以速度v垂直磁感应强度为B的匀强磁场由.P点进入,界面I和Ⅱ平行,宽度为L(L<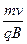 )要使离子由界面II飞出可改变离子的入射方向,离子所受重力不计,求离子在磁场中运动时间的最小值和最大值
)要使离子由界面II飞出可改变离子的入射方向,离子所受重力不计,求离子在磁场中运动时间的最小值和最大值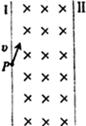
如图所示,在xOy平面内y>0的区域中存在垂直纸面向外的匀强磁场,磁感应强度大小为B0,在y<0的区域也存在垂直纸面向外的匀强磁场(图中未画出),一带正电的粒子从y轴上的P点垂直磁场入射,速度方向与y轴正向成45¡。粒子第一次进入y<0的区域时速度方向与x轴正向成135¡,再次在y>0的区域运动时轨迹恰与y轴相切。已知OP的距离为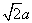 ,粒子的重力不计,求:
,粒子的重力不计,求: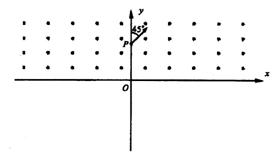
(1)y<0的区域内磁场的磁感应强度大小;
(2)粒子第2n(n∈N+)次通过x轴时离O点的距离(本问只需写出结果)。
两平面荧光屏互相垂直放置,在两屏内分别取垂直于两屏交线的直线为x轴和y轴,交点O为原点,如图所示,在y>0,0<x<a的区域有垂直于纸面向里的匀强磁场,在y>0,x>a的区域有垂直于纸面向外的匀强磁场,两区域内的磁感应强度大小均为B。在O点有一处小孔,一束质量为m、带电量为q(q>0)的粒子沿x轴经小孔射入磁场,最后打在竖直和水平荧光屏上,使荧光屏发亮,入射粒子的速度可取从零到某一最大值之间的各种数值。已知速度最大的粒子在0<x<a的区域中运动的时间与在x>a的区域中运动的时间之比为2:5,在磁场中运动的总时间为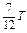 ,其中T为该粒子在磁感应强度为B的匀强磁场中作圆周运动的周期。试求两个荧光屏上亮线的范围(不计重力的影响)。
,其中T为该粒子在磁感应强度为B的匀强磁场中作圆周运动的周期。试求两个荧光屏上亮线的范围(不计重力的影响)。
(19分)如图所示,在xoy平面内,以O'(0,R)为圆心、R为半径的圆内有垂直平面向外的匀强磁场,x轴下方有垂直平面向里的匀强磁场,两区域磁感应强度大小相等。第四象限有一与x轴成45°角倾斜放置的挡板PQ,P、Q两点在坐标轴上,且OP两点间的距离大于2R,在圆形磁场的左侧0<y<2R的区间内,均匀分布着质量为m、电荷量为+q的一簇带电粒子,当所有粒子均沿x轴正向以速度v射入圆形磁场区域时,粒子偏转后都从O点进人x轴下方磁场,结果有一半粒子能打在挡板上。不计粒子重力、不考虑粒子间相互作用力。求:
(1)磁场的磁感应强度B的大小;
(2)挡板端点P的坐标;
(3)挡板上被粒子打中的区域长度。
在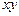 平面上有一片稀疏的电子处在
平面上有一片稀疏的电子处在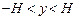 的范围内,从
的范围内,从 负半轴的远处以相同的速率
负半轴的远处以相同的速率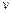 沿着
沿着 轴方向平行地向
轴方向平行地向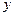 轴射来. 试设计一个磁场,使得所有电子均通过原点,然后扩展到在
轴射来. 试设计一个磁场,使得所有电子均通过原点,然后扩展到在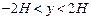 范围内继续沿着
范围内继续沿着 正方向飞行(如图,虚线内范围)
正方向飞行(如图,虚线内范围)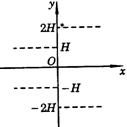
如图所示,在平面直角坐标系xOy中,第I象限存在沿y轴负方向的匀强电场,第IV象限存在垂直于坐标平面向外的匀强磁场,一带正电的粒子从y轴正半轴上的M点以速度v0垂直于y轴射入电场,经偏转电场后到达x轴上的N点,然后射入磁场,最后从y轴负半轴上的P点垂直于y轴射出磁场,已知M点的坐标是(0,h),N点的坐标是(2h,0),不计粒子重力,求: 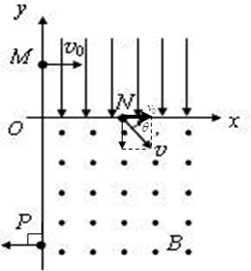
(1)粒子到达N点时的速度v的大小以及v与初速度v0的夹角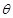 ;
;
(2)粒子在磁场中运动的轨道半径r;
(3)粒子从M点运动到P点的总时间t。
汤姆生曾采用电场、磁场偏转法测定电子的比荷,具体方法如下:
Ⅰ.使电子以初速度v1垂直通过宽为L的匀强电场区域,测出偏向角θ,已知匀强电场的场强大小为E,方向如图(a)所示 Ⅱ.使电子以同样的速度v1垂直射入磁感应强度大小为B、方向如图(b)所示的匀强磁场,使它刚好经过路程长度为L的圆弧之后射出磁场,测出偏向角φ,请继续完成以下三个问题:
Ⅱ.使电子以同样的速度v1垂直射入磁感应强度大小为B、方向如图(b)所示的匀强磁场,使它刚好经过路程长度为L的圆弧之后射出磁场,测出偏向角φ,请继续完成以下三个问题:
(1)电子通过匀强电场和匀强磁场的时间分别为多少?
(2)若结果不用v1表达,那么电子在匀强磁场中做圆弧运动对应的圆半径R为多少?
(3)若结果不用v1表达,那么电子的比荷e / m为多少?
如图所示,K与虚线MN之间是加速电场,虚线MN与PQ之间是匀强电场,虚线PQ与荧光屏之间是匀强磁场,且MN、PQ与荧光屏三者互相平行,电场和磁场的方向如图所示,图中A点与O点的连线垂直于荧光屏.一带正电的粒子从A点离开加速电场,速度方向垂直于偏转电场方向射入偏转电场,在离开偏转电场后进入匀强磁场,最后恰好垂直地打在荧光屏上.已知电场和磁场区域在竖直方向足够长,加速电场电压与偏转电场的场强关系为U=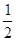 Ed,式中的d是偏转电场的宽度,磁场的磁感应强度B与偏转电场的电场强度E和带电粒子离开加速电场的速度v0关系符合表达式v0=
Ed,式中的d是偏转电场的宽度,磁场的磁感应强度B与偏转电场的电场强度E和带电粒子离开加速电场的速度v0关系符合表达式v0=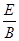 .若题中只有偏转电场的宽度d为已知量。
.若题中只有偏转电场的宽度d为已知量。
(1)画出带电粒子轨迹示意图。
(2)磁场的宽度L为多少?
(3)带电粒子在电场和磁场中垂直于v0方 向的偏转距离分别是多少?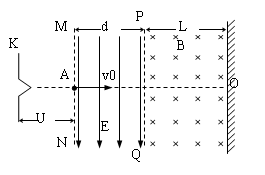
如图3-2-8所示,一质量为0.4kg足够长且粗细均匀的绝缘细管置于水平地面上,细管内表面粗糙,外表面光滑;有一质量为0.1kg、电量为0.1C的带正电小球沿管以水平向右的速度进入管内,细管内径略大于小球直径,已知细管所在位置有水平方向垂直于管向里的匀强磁场,磁感强度为1T(g=10m/s2)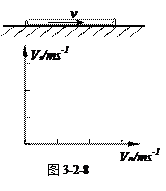
当细管固定不动时,在(乙图)中画出小球在管中运动初速度和最终稳定的速度的关系图象.取水平向右为正方向.
若细管不固定,带电小球以20m/s的初速度进入管内,且整个运动过程中细管没有离开地面,则系统最终产生的内能为多少?
如图所示,M、N为水平放置的平行金属板,板长和板间距均为2d。在金属板左侧板间中点处有电子源S,能水平发射初速为v0的电子,电子的质量为m,电荷量为e。金属板右侧有两个磁感应强度大小始终相等,方向分别垂直于纸面向外和向里的匀强磁场区域,两磁场的宽 度均为d。磁场边界与水平金属板垂直,左边界紧靠金属板右侧,距磁场右边界d处有一个荧光屏。过电子源S作荧光屏的垂线,垂足为O。以O为原点,竖直向下为正方向,建立y轴。现在M、N两板间加上图示电压,使电子沿SO方向射入板间后,恰好能够从金属板右侧边缘射出.进入磁场。(不考虑电子重力和阻力)
(1)电子进人磁场时的速度v;
(2)改变磁感应强度B的大小,使电子能打到荧光屏上,求:
①磁场的磁感应强度口大小的范围;
②电子打到荧光屏上位置坐标的范围。
如图所示,有一半径为r的圆形有界匀强磁场区域,磁感应强度为B,方向垂直纸面向里,其周围对称放置带有中心孔a、b、c的三个相同的平行板电容器,三个电容器两板间距离均为d,接有相同的电压U,在D处有一静止的电子,质量为m,电荷量为e,释放后从a孔射入匀强磁场中,并先后穿过b、c孔再从a孔穿出回到D处,求:
(1)电子在匀强磁场中运动的轨道半径R;
(2)匀强磁场的磁感应强度B;
(3)电子从D出发到第一次回到D处所用的时间t。
在平面直角坐标系xOy中,第Ⅰ象限存在沿y轴负方向的匀强电场,第Ⅳ象限存在垂直于坐标平面向里的匀强磁场,磁感应强度为B,一质量为m、电荷量为q的带正电的粒子经过加速电场加速从y轴正半轴上的A点以某速度垂直于y轴射入电场,经x轴上的M点与x轴正方向成θ角射入磁场,从x轴上的N点离开磁场,MN之间的距离为l,(不计粒子重力),求: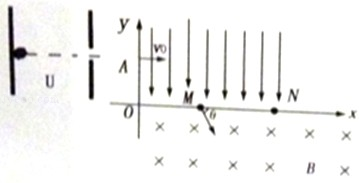
(1)粒子在磁场中速度v大小;
(2)加速电场的电压;
(3)若A点到x轴的高度OA=h,求匀强电场的电场强度.
如图所示的平面直角坐标系中,在y>0的区域存在匀强电场,场强沿y轴负方向,在y<0的区域存在匀强磁场,磁场方向垂直于坐标平面向外。一电荷量为q、质量为m的带正电粒子,经过y轴上y=h处的点Pl时速率为vo,方向沿x轴正方向;然后经过x轴上x=2h处的P2点进入磁场。不计粒子重力。
(1)求电场强度的大小;
(2)若粒子进人磁场后,接着经过了y轴上y=-2h处的P3点,求磁感应强度的大小;
(3)若只改变磁场的大小(仍为匀强磁场),让粒子仍从Pl经P2沿原路径进入磁场后,为了使粒子能再次通过P2点,求磁感应强度的大小满足的条件。