(4分)如图所示,矩形区域宽度为l,其内有磁感应强度为B、垂直纸面向外的匀强磁场.一带电粒子以初速度v0垂直左边界射入,飞出磁场时偏离原方向300.若撤去原来的磁场,在此区域内加一个电场强度为E、方向竖直向下的匀强电场(图中未画出),带电粒子仍以原来的初速度入射.不计粒子的重力,求:
(1)带电粒子在磁场中的运动半径;
(2)带电粒子在磁场中运动的时间;
(3)带电粒子飞出电场后的偏转角.
如图甲所示,在坐标系x轴上P点到O点之间存在竖直方向如图乙所示的交变电场,规定竖直向上为正方向,其中T已知,E0未知,在y轴右边存在一半径为R的圆形匀强磁场区域,圆心在(R,0)处,磁感应强度大小为B,方向垂直于纸面向外。一电荷量为q(q>0),质量为m的粒子在t=0时从M点沿平行于x轴正方向射入电场区域,然后从y轴上的N点沿平行于x轴正方向射出电场区域。M点与N点距的x轴距离均为 ,已知粒子射出磁场与射入磁场时运动方向间的夹角为60°,不计粒子重力,求:
,已知粒子射出磁场与射入磁场时运动方向间的夹角为60°,不计粒子重力,求:
(1)粒子射入电场时的速度大小;
(2)O、P两点间的距离应满足的条件;
(3)电场强度E0应满足的条件。
磁谱仪是测量α能谱的重要仪器。磁谱仪的工作原理如图所示,放射源S发出质量为m、电量为q的α粒子沿垂直磁场方向进入磁感应强度为B的匀强磁场,被限束光栏Q限制在2φ的小角度内,α粒子经磁场偏转后打到与束光栏平行的感光片P上。(重力影响不计)
⑴若能量在E~E+ΔE(ΔE>0,且 )范围内的α粒子均垂直于限束光栏的方向进入磁场。试求这些α粒子打在胶片上的范围Δx1。
)范围内的α粒子均垂直于限束光栏的方向进入磁场。试求这些α粒子打在胶片上的范围Δx1。
⑵实际上,限束光栏有一定的宽度,α粒子将在2φ角内进入磁场。试求能量均为E的α 粒子打到感光胶片上的范围Δx2 
如图所示,两水平放置的平行金属板a、b,板长L=0.2 m,板间距d=0.2 m.两金属板间加可调控的电压U,且保证a板带负电,b板带正电, 忽略电场的边缘效应.在金属板右侧有一磁场区域,其左右总宽度s=0.4 m,上下范围足够大,磁场边界MN和PQ均与金属板垂直,磁场区域被等宽地划分为n(正整数)个竖直区间,磁感应强度大小均为B=5×10-3T,方向从左向右为垂直纸面向外、向内、向外…….在极板左端有一粒子源,不断地向右沿着与两板等距的水平线OO′发射比荷 =1×108 C/kg、初速度为v0=2×105 m/s的带正电粒子。忽略粒子重力以及它们之间的相互作用.
=1×108 C/kg、初速度为v0=2×105 m/s的带正电粒子。忽略粒子重力以及它们之间的相互作用.
(1)当取U何值时,带电粒子射出电场时的速度偏向角最大;
(2)若n=1,即只有一个磁场区间,其方向垂直纸面向外,则当电压由0连续增大到U过程中带电粒子射出磁场时与边界PQ相交的区域的宽度;
(3)若n趋向无穷大,则偏离电场的带电粒子在磁场中运动的时间t为多少?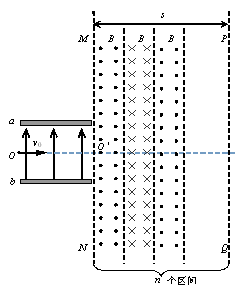
如题图所示,在半径为a的圆柱空间中(图中圆为其横截面)充满磁感应强度大小为B的均匀磁场,其方向平行于轴线远离读者.在圆柱空间中垂直轴线平面内固定放置一绝缘材料制成的边长为L=1.6a的刚性等边三角形框架ΔDEF,其中心O位于圆柱的轴线上.DE边上S点( )处有一发射带电粒子的源,发射粒子的方向皆在图题图中截面内且垂直于DE边向下。发射粒子的电量皆为q(>0),质量皆为m,但速度v有各种不同的数值。若这些粒子与三角形框架的碰撞无能量损失,电量也无变化,且每一次碰撞时速度方向均垂直于被碰的边。试问:
)处有一发射带电粒子的源,发射粒子的方向皆在图题图中截面内且垂直于DE边向下。发射粒子的电量皆为q(>0),质量皆为m,但速度v有各种不同的数值。若这些粒子与三角形框架的碰撞无能量损失,电量也无变化,且每一次碰撞时速度方向均垂直于被碰的边。试问: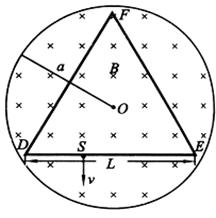
(1)带电粒子经多长时间第一次与DE边相碰?
(2)带电粒子速度v的大小取哪些数值时可使S点发出的粒子最终又回到S点?
(3)这些粒子中,回到S点所用的最短时间是多少?

如图,在区域内存在与
平面垂直的匀
 强磁场,磁感应强度的大小为
强磁场,磁感应强度的大小为.在
时刻,一位于坐标原点的粒子源在
平面内发射出大量同种带电粒子,所有粒子的初速度大小相同,方向与
轴正方向的
 夹角分布在
夹角分布在范围内。已知沿y轴正方向发射的粒子在
时刻刚好从磁场边界上
点离开磁场。求:
⑴ 粒子在磁场中做 圆周运动的半径
圆周运动的半径及粒子的比荷
;
⑵ 此时刻仍在磁场中的粒子的初速度方向与轴正方向夹角的取值范围;
⑶ 从粒子发射到全部粒子离开磁场所用的时间。
如图所示,在正三角形区域内存在着垂直于纸面的匀强磁场和平行于AB的水平方向的匀强电场,一不计重力的带电粒子刚好以某一初速度从三角形O点沿角分线OC做匀速直线运动。若此区域只存在电场时,该粒子仍以此初速度从O点沿角分线OC射入,则此粒子刚好从A点射出;若只存在磁场时,该粒子仍以此初速度从O点沿角分线OC射入,则下列说法正确的是:
| A.粒子将在磁场中做匀速圆周运动,运动轨道半径等于三角形的边长 |
| B.粒子将在磁场中做匀速圆周运动,且从OB阶段射出磁场 |
| C.粒子将在磁场中做匀速圆周运动,且从BC阶段射出磁场 |
| D.根据已知条件可以求出该粒子分别在只有电场时和只有磁场时在该区域中运动的时间之比 |
(12分)在如图所示的直角坐标系xoy中,矩形区域oabc内有垂直于纸面向外的匀强磁场,磁感应强度大小为B=5.0×10-2T;第一象限内有沿-y方向的匀强电场,电场强度大小为E=1.0×105N/C.已知矩形区域oa边长为0.60m,ab边长为0.20 m.在bc边中点N处有一放射源,某时刻,放射源沿纸面向磁场中各方向均匀地辐射出速率均为 m/s的某种带正电粒子,带电粒子质量m=1.6×10-27kg,电荷量为q=+3.2×10-19kg,不计粒子重力,求:(计算结果保留两位有效数字)
m/s的某种带正电粒子,带电粒子质量m=1.6×10-27kg,电荷量为q=+3.2×10-19kg,不计粒子重力,求:(计算结果保留两位有效数字)
(1)粒子在磁场中运动的半径;
(2)从x轴上射出的粒子中,在磁场中运动的最短路程为多少?
(3)放射源沿-x方向射出的粒子,从射出到从y轴离开所用的时间.
用磁聚焦法测比荷的装置如图所示.在真空玻璃管中装有热阴极K和带有小孔的阳极A.在A、K之间加上电压U后,不断地有电子从阴极K由静止加速到达阳极A,并从小孔射出.接着电子进入平行板电容器C,电容器两极板间加有不大的交变电场,使不同时刻通过的电子发生不同程度的偏转;电容器C和荧光屏S之间加一水平向右的均匀磁场,电容器和荧光屏间的距离为L,电子经过磁场后打在荧光屏上,将磁场的磁感应强度从零开始缓慢增大到为B时,荧光屏上的光点的锐度最大(这时荧光屏S上的亮斑最小).
(1)若平行板电容器C的板长为 ,求电子经过电容器和磁场区域的时间之比;
,求电子经过电容器和磁场区域的时间之比;
(2)用U、B、L表示出电子的比荷;
(3)在磁场区域再加一匀强电场,其电场强度的大小为 ,方向与磁场方向相反,若保持U、L和磁场方向不变,调节磁场的磁感应强度大小,仍使电子在荧光屏上聚焦,则磁感应强度大小满足的条件是什么?
,方向与磁场方向相反,若保持U、L和磁场方向不变,调节磁场的磁感应强度大小,仍使电子在荧光屏上聚焦,则磁感应强度大小满足的条件是什么?
如图所示,半径为R的半圆形区域内分布着垂直纸面向里的匀强磁场,磁感应强度为B,半圆的左边垂直x轴放置一粒子发射装置,在-R≤y≤R的区间内各处均沿x轴正方向同时发射出一个带正电粒子,粒子质量均为m、电荷量均为q初速度均为v,重力及粒子间的相互作用均忽略不计,所有粒子都能到达y轴,其中最后到达y轴的粒子比最先到达y轴的粒子晚Δt时间,则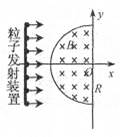
| A.粒子到达y轴的位置一定各不相同 |
B.磁场区域半径R应满足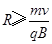 |
C.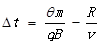 ,其中角度θ的弧度值满足 ,其中角度θ的弧度值满足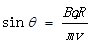 |
D.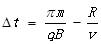 |
大型强子对撞机是研究高能粒子的重要工具,同种物质的正反粒子由静止开始经电压为U的直线加速器加速后,沿切线方向进入对撞机的真空环状空腔内,空腔内存在与圆环平面垂直的匀强磁场,磁感应强度为B,两种粒子在环形空腔内沿相反方向作半径为r的匀速圆周运动,进而实现碰撞。下列说法正确的是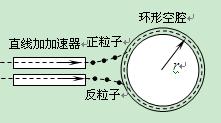
A.对于给定的加速电压,带电粒子的比荷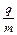 越大,磁感应强度B越大 越大,磁感应强度B越大 |
B.对于给定的加速电压,带电粒子的比荷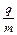 越大,磁感应强度B越小 越大,磁感应强度B越小 |
| C.对于给定的带电粒子,加速电压U越大,粒子运动的周期越大 |
| D.对于给定的带电粒子,不管加速电压U多大,粒子运动的周期都不变 |
如图甲所示,在空心三棱柱CDF以外足够大的空间中,充满着磁感应强度为B的匀强磁场。三棱柱的轴线与磁场平行,截面边长为L,三棱柱用绝缘薄板材料制成,其内部有平行于CD侧面的金属板P、Q,两金属板间的距离为d,P板带正电,Q板带负电,Q板中心有一小孔,P板上与小孔正对的位置有一个粒子源S,从S处可以发出初速度为0、带电量为+q、质量为m的粒子,这些粒子与三棱柱侧面碰撞时无能量损失。试求:
(1)为使从S点发出的粒子最终又回到S点,P、Q之间的电压U应满足什么条件?(Q与CD之间距离不计)
(2)粒子从S点出发又回到S点的最短时间是多少?
(3)若磁场是半径为a的圆柱形区域,如图乙所示,圆柱的轴线与三棱柱的轴线重合,且a=( +
+ )L,要使S点发出的粒子最终又回到S点,则P、Q之间的电压不能超过多少?
)L,要使S点发出的粒子最终又回到S点,则P、Q之间的电压不能超过多少?
如图所示. 半径分别为a、b的两同心虚线圆所围区域分别存在电场和磁场,中心O处固定一个半径很小(可忽略不计)的金属球,在小圆空间内存在沿水平的径向辐向电场。小圆周与金属球间电势差为U,两圆之间存在垂直于纸面向里的匀强磁场,设有一个带负电的粒子从金属球表面沿x轴正方向以很小的初速度逸出,粒子质量为m,电荷量为q.(不计粒子的重力,忽略粒子逸出的初速度)求:
(1)粒子到达小圆周上时的速度为多大?
(2)粒子以(1)中的速度进入两圆间的磁场中,当磁感应强超过某一临界值时,粒子将不能到达大圆周,求此磁感应强度的最小值B.
(3)若磁感应强度取(2)中最小值,且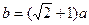 ,要使粒子恰好第一次沿逸出方向的反方向回到原出发点,粒子需经过多少次回旋?并求粒子在磁场中运动的时间.(设粒子与金属球正碰后电量不变且能以原速率原路返回)
,要使粒子恰好第一次沿逸出方向的反方向回到原出发点,粒子需经过多少次回旋?并求粒子在磁场中运动的时间.(设粒子与金属球正碰后电量不变且能以原速率原路返回)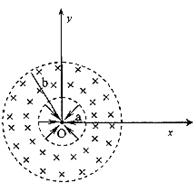
21.(19分)
图为“双聚焦分析器”质谱仪的结构示意图,其中,加速电场的电压为U,静电分析器中与圆心01等距离的各点场强大小相等、方向沿径向,磁分析器中以02为圆心、圆心角为90o的扇形区域内,分布着方向垂直于纸面的匀强磁场,其左边界与静电分析器的右端面平行。由离子源发出的一质量为m、电荷量为g的正离子(初速度为零,重力不计)经加速电场加速后,从M点垂直于电场方向进入静电分析器,沿半径为R的四分之一圆弧轨迹做匀速圆周运动,从N点射出,接着由P点垂直磁分析器的左边界射入,最后垂直于下边界从Q点射出并进入收集器。已知Q点与圆心02的距离为d。求:
(1)磁分析器中磁场的磁感应强度B的大小和方向;
(2)静电分析器中离子运动轨迹处电场强度E的大小;
(3)现将离子换成质量为0.9m、电荷量仍为g的另一种正离子,其它条件不变。试直接指出该离子进入磁分析器时的位置,它射出磁场的位置在Q点的左侧还是右侧?