如图所示，M、N是竖直正对放置的两个平行金属板，S1、S2是M、N板上的两个小孔；N板的右侧有一个在竖直面内，以O为圆心的圆形区域，该区域内存在垂直圆面向外的匀强磁场，另有一个同样以O为圆心的半圆形荧光屏AO＇C已知S1、S2、O和荧光屏的中间位置O＇在同一直线上，且AC⊥S1O＇。当在M、N板间加恒定电压U时，一带正电离子在S1处由静止开始加速向S2孔运动，最后打在图示的荧光屏上P处，∠COP=30°。若要让上述带正电离子(不计重力)仍在S1处由静止开始加速，最后打在图示的荧光屏下边缘Ｃ处，求M、N板间所加电压的大小。
如图所示，在x轴上方有垂直于xy平面向里的匀强磁场，磁感应强度为B；在x轴下方有沿y轴负方向的匀强电场，场强为E。一质量为m，电荷量为-q的粒子从坐标原点O沿着y轴正方向射出。射出之后，第三次到达x轴时，它与点O的距离为L。
（1）求此粒子射出时的速度v
（2）运动的总路程s（重力不计）。
如图所示，第二、三象限存在足够大的匀强电场，电场强度为E，方向平行于纸面向上，一个质量为m，电量为q的正粒子，在x轴上M点(－4r，0)处以某一水平速度释放，粒子经过y轴上N点(0，2r)进入第一象限，第一象限存在一个足够大的匀强磁场，其磁感应强度B＝2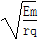
，方向垂直于纸面向外，第四象限存在另一个足够大的匀强磁场，其磁感应强度B＝2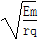，方向垂直于纸面向里，不计粒子重力，r为坐标轴每个小格的标度，试求：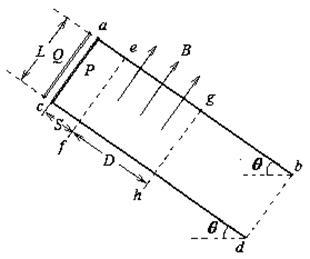
(1)粒子初速度v0；
(2)粒子第1次穿过x轴时的速度大小和方向；
(3)画出粒子在磁场中运动轨迹并求出粒子第n次穿过x轴时的位置坐标。
如图所示，直角三角形ABC区域中存在一匀强磁场，比荷相同的两个粒子（不计重力）沿AB方向射入磁场，分别从AC边上的P、Q两点射出，则（ ）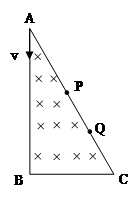
| A．从P点射出的粒子速度大 |
| B．从Q点射出的粒子速度大 |
| C．从Q点射出的粒子在磁场中运动的时间长 |
| D．两个粒子在磁场中运动的时间一样长 |
如图所示，在边长为a的正方形ABCD的对角线AC左右两侧，分别存在垂直纸面向内磁感应强度为B的匀强磁场和水平向左电场强度大小为E的匀强电场， AD、CD是两块固定荧光屏（能吸收打到屏上的粒子）。现有一群质量为m、电量为q的带正电粒子，从A点沿AB方向以不同速率连续不断地射入匀强磁场中，带电粒子速率范围为 
。已知
，不计带电粒子的重力和粒子之间的相互作用。求：
（1）恰能打到荧光屏C D上的带电粒子的入射速度；
（2）AD、CD两块荧光屏上形成亮线的长度。
如图所示，三个速度大小不同的同种带电粒子，沿同一方向从图中长方形区域的匀强磁场上边缘射入，当它们从下边缘飞出时对入射方向的偏角分别为90°、60°、30°，则它们的初速度大小之比为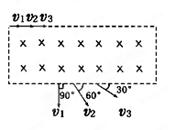
| A．1∶1∶1 | B．1∶2∶3 | C．1∶2∶4 | D．1∶2∶（4+2） |
边长为a的正方形，处于有界磁场如图所示，一束电子以水平速度射入磁场后，分别从A处和C处射出，则vA：vC=__________;所经历的时间之比tA：tC=___________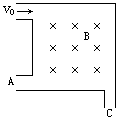
如图，在x轴上方存在垂直纸面向里的磁感应强度为B的匀强磁场，x轴下方存在垂直纸面向外的磁感应强度为
的匀强磁场，一带负电的粒子从原点O以与x轴成30°角斜向上的速度射入磁场，且在上方运动半径为R则（不计重力）（ ）
| A．粒子经偏转一定能回到原点O |
B．粒子在x轴上方和下方两磁场中运动的半径之比为 |
C．粒子完在成一次周期性运动的时间为 |
| D．粒子第二次射入x轴上方磁场时，沿x轴前进3R |
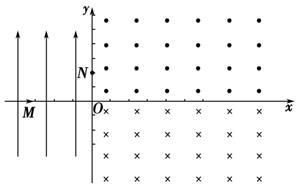
如图所示，PQ、MN两极板间存在匀强电场，MN极板右侧的长为
，宽为2L的虚线区域内有垂直纸面的匀强磁场B。现有一初速度为零、带电量为q、质量为m的离子(不计重力)从PQ极板出发，经电场加速后，从MN上的小孔A垂直进入磁场区域，并从NF边界上某点垂直于虚线边界射出。求：
(1)匀强磁场的方向；
(2)PQ、MN两极板间电势差U；
(3)若带点粒子能从NF边界射出，则PQ、MN两极板间电势差的范围是多少？
如图所示的虚线框为一长方形区域，该区域内有一垂直于纸面向里的匀强磁场，一束电子以不同的速率从O点垂直于磁场方向、沿图中方向射入磁场后，分别从a、b、c、d四点射出磁场，比较它们在磁场中的运动时间ta、tb、tc、td，其大小关系是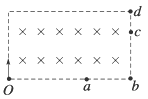
| A．ta<tb<tc<td |
| B．ta＝tb＝tc＝td |
| C．ta＝tb>td>tc |
| D．ta＝tb>tc>td |
两个质量相同、所带电荷量相等的带电粒子 a、b，以不同的速率对准圆心 O沿着 AO方向射入圆形匀强磁场区域，其运动轨迹如图所示．若不计粒子的重力，则下列说法正确的是（ ）
| A．a粒子带负电，b粒子带正电 |
| B．a粒子在磁场中所受洛伦兹力较大 |
| C．b粒子动能较大 |
| D．b粒子在磁场中运动时间较长 |
如图（甲）所示，在场强大小为E、方向竖直向上的匀强电场中存在着一半径为R的圆形区域，O点为该圆形区域的圆心，A点是圆形区域的最低点，B点是圆形区域最右侧的点。在A点有放射源释放出初速度大小不同、方向均垂直于场强方向向右的正电荷，电荷的质量为m、电量为q，不计电荷重力、电荷之间的作用力。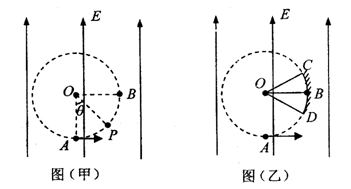
（1）某电荷的运动轨迹和圆形区域的边缘交于P点，如图（甲）所示，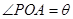
，求该电荷从A点出发时的速率。
（2）若在圆形区域的边缘有一接收屏CBD，如图（乙）所示，C、D分别为接收屏上最边缘的两点，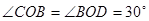
，求该屏上接收到的电荷的最大动能和最小动能。
如图所示，在一底边长为2L，底角θ =45°的等腰三角形区域内（O为底边中点）有垂直纸面向外的匀强磁场。现有一质量为m，电量为q的带正电粒子从静止开始经过电势差为U的电场加速后，从O点垂直于AB进人磁场，不计重力与空气阻力的影响。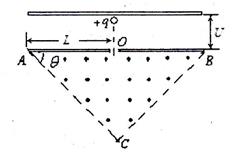
（1）求粒子经电场加速射人磁场时的速度；
（2）若要进人磁场的粒子能打到OA板上，求磁感应强度B的最小值；
（3）设粒子与AB板碰撞后，电量保持不变并以与碰前相同的速率反弹。磁感应强度越大，粒子在磁场中的运动时间也越大。求粒子在磁场中运动的最长时间。
如图所示，在倾角为30°的斜面OA的左侧有一竖直档板，其上有一小孔P，OP=0.5m．现有一质量m=4×10﹣20kg，带电量q=+2×10﹣14C的粒子，从小孔以速度v0=3×104m/s水平射向磁感应强度B=0.2T、方向垂直纸面向外的一圆形磁场区域．且在飞出磁场区域后能垂直打在OA面上，粒子重力不计．
求：
（1）粒子在磁场中做圆周运动的半径；
（2）粒子在磁场中运动的时间；
（3）圆形磁场区域的最小半径．
如图所示，倾角为θ的足够长光滑绝缘斜面上存在宽度均为L的匀强电场和匀强磁场区域，电场的下边界与磁场的上边界相距为L，其中电场方向沿斜面向上，磁场方向垂直于斜面向下、磁感应强度的大小为B。电荷量为q的带正电小球（视为质点）通过长度为4L的绝缘轻杆与边长为L、电阻为R的正方形单匝线框相连，它们的总质量为m，置于斜面上，线框下边与磁场的上边界重合。现将该装置由静止释放，当线框下边刚离开磁场时恰好做匀速运动；当小球运动到电场的下边界时速度恰好减为0。已知L=1m，B=0.8T，q=2.2×10-6C，R=0.1Ω，m=0.8kg，θ=53°，sin53°=0.8，取g=10m/s2。求：
（1）线框做匀速运动时的速度v；
（2）电场强度E的大小；
（3）足够长时间后小球到达的最低点与电场上边界的距离x。
粤公网安备 44130202000953号