如图所示,在边长为a的正方形ABCD的对角线AC左右两侧,分别存在垂直纸面向内磁感应强度为B的匀强磁场和水平向左电场强度大小为E的匀强电场, AD、CD是两块固定荧光屏(能吸收打到屏上的粒子)。现有一群质量为m、电量为q的带正电粒子,从A点沿AB方向以不同速率连续不断地射入匀强磁场中,带电粒子速率范围为 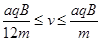 。已知
。已知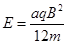 ,不计带电粒子的重力和粒子之间的相互作用。求:
,不计带电粒子的重力和粒子之间的相互作用。求: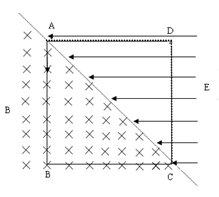
(1)恰能打到荧光屏C D上的带电粒子的入射速度;
(2)AD、CD两块荧光屏上形成亮线的长度。
如图所示,在边长为a的正方形ABCD的对角线AC左右两侧,分别存在垂直纸面向内磁感应强度为B的匀强磁场和水平向左电场强度大小为E的匀强电场, AD、CD是两块固定荧光屏(能吸收打到屏上的粒子)。现有一群质量为m、电量为q的带正电粒子,从A点沿AB方向以不同速率连续不断地射入匀强磁场中,带电粒子速率范围为 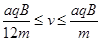 。已知
。已知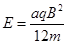 ,不计带电粒子的重力和粒子之间的相互作用。求:
,不计带电粒子的重力和粒子之间的相互作用。求:
(1)恰能打到荧光屏C D上的带电粒子的入射速度;
(2)AD、CD两块荧光屏上形成亮线的长度。