如图所示,一根细线下端拴一个金属小球 ,细线的上端固定在金属块
,细线的上端固定在金属块 上,
上, 放在带小孔(小孔光滑)的水平桌面上,小球在某一水平面内做匀速圆周运动(圆锥摆)。现使小球改到一个更高一些的水平面上做匀速圆周运动(图中
放在带小孔(小孔光滑)的水平桌面上,小球在某一水平面内做匀速圆周运动(圆锥摆)。现使小球改到一个更高一些的水平面上做匀速圆周运动(图中 位置),两次金属块
位置),两次金属块 都静止在桌面上的同一点,则后一种情况与原来相比较,下面的判断中正确的是
都静止在桌面上的同一点,则后一种情况与原来相比较,下面的判断中正确的是
| A.细线所受的拉力变小 | B.小球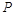 运动的角速度变小 运动的角速度变小 |
C. 受到桌面的静摩擦力变大 受到桌面的静摩擦力变大 |
D. 受到桌面的支持力变大 受到桌面的支持力变大 |
如图所示,固定在竖直面内的光滑圆环半径为R,圆环上套有质量分别为m和2m的小球A、B(均可看作质点),且小球A、B用一长为2R的轻质细杆相连,在小球B从最高点由静止开始沿圆环下滑至最低点的过程中(已知重力加速度为g),下列说法正确的是
A.A球增加的机械能等于B球减少的机械能
B.A球增加的重力势能等于B球减少的重力势能
C.A球的最大速度为
D.细杆对A球做的功为 mgR
mgR
如图所示,光滑水平轨道与半径为R的光滑竖直半圆轨道在B点平滑连接.在过圆心O的水平界面MN的下方分布有水平向右的匀强电场.现有一个质量为m、电荷量为q的带正电小球在水平轨道上的A点由静止释放,小球运动到C点离开半圆轨道后,经界面MN上的P点进入电场(P点恰好在A点的正上方,小球可视为质点,小球运动到C点之前所带电荷量保持不变,经过C点后所带电荷量立即变为零).已知A、B两点间的距离为2R,重力加速度为g.在上述运动过程中,求:

(1)电场强度E的大小;
(2)小球在半圆轨道上运动时的最大速率.
北斗卫星导航系统空间段计划由35颗卫星组成,包括5颗静止轨道卫星、27颗中地球轨道卫星、3颗倾斜同步轨道卫星。中地球轨道卫星和静止轨道卫星都绕地球球心做圆周运动,中地球轨道卫星离地面高度低,则中地球轨道卫星与静止轨道卫星相比,做圆周运动的
| A.向心加速度大 | B.周期大 | C.线速度小 | D.角速度小 |
如图所示,长为3L的轻杆课绕水平转轴O转动,在杆两端分别固定质量均为m的球A、B(可视为质点),球A距轴O的距离为L。现给系统一定动能,使杆和球在竖直平面内转动。当球B运动到最高点时,水平转轴O对杆的作用力恰好为零,忽略空气阻力。已知重力加速度为g,则球B在最高点时,下列说法正确的是

A.球B的速度为0 B.杆对球B的弹力为0
C.球B的速度为 D.球A的速度等于
D.球A的速度等于
如图所示,一质量为M的光滑大圆环,用一细轻杆固定在竖直平面内;套在大圆环上的质量为m的小环(可视 为质点),从大圆环的最高处由静止滑下,重力加速度为g。当小圆环滑到大圆环的最低点时,大圆环对轻杆拉力的大小为
| A.Mg-5mg |
| B.Mg+mg |
| C.Mg+5mg |
| D.Mg+10mg |
在水平公路上行驶的汽车,转弯时提供向心力的是( )
| A.汽车所受的重力 |
| B.汽车所受的支持力 |
| C.汽车所受的摩擦力 |
| D.汽车所受的重力和支持力的合力 |
如图所示,在竖直平面的xoy坐标系内,一根长为l的不可伸长的细绳,一端固定在拉力传感器A上,另一端系一质量为m的小球.x轴上的P点固定一个表面光滑的小钉,P点与传感器A相距 .现拉小球使细绳绷直并处在水平位置,然后由静止释放小球,当细绳碰到钉子后,小球可以绕钉子在竖直平面内做圆周运动.已知重力加速度大小为g,求:
.现拉小球使细绳绷直并处在水平位置,然后由静止释放小球,当细绳碰到钉子后,小球可以绕钉子在竖直平面内做圆周运动.已知重力加速度大小为g,求:
(1)若小球经过最低点时拉力传感器的示数为7mg,求此时小球的速度大小;
(2)传感器A与坐标原点O之间的距离;
(3)若小球经过最低点时绳子恰好断开,请确定小球经过y轴的位置.
如图所示,竖直平面内四分之一光滑圆弧轨道AP和水平传送带PC相切于P点,圆弧轨道的圆心为O,半径为R=5m,一质量为m=2kg的小物块从圆弧顶点由静止开始沿轨道下滑,再滑上传送带PC,传送带可以速度v=5m/s沿顺时针或逆时针方向的传动.小物块与传送带间的动摩擦因数为μ=0.5,不计物体经过圆弧轨道与传送带连接处P时的机械能损失,重力加速度为g=10m/s2.
(1)求小物体滑到P点时对圆弧轨道的压力;
(2)若传送带沿逆时针方向传动,物块恰能滑到右端C,问传送带PC之间的距离L为多大.
“飞车走壁”是一种传统的杂技艺术,演员骑车在倾角很大的桶面上做圆周运动而不掉下来.如图所示,已知桶壁的倾角为θ,车和人的总质量为m,做圆周运动的半径为r,若使演员骑车做圆周运动时不受桶壁的摩擦力,下列说法正确的是( )

A.人和车的速度为 |
B.人和车的速度为 |
C.桶面对车的弹力为 |
D.桶面对车的弹力为 |
如图所示,小球质量为m,用长为L的轻质细线悬挂在O点,在O点的正下方 处有一钉子P,把细线沿水平方向拉直,无初速度地释放小球,当细线碰到钉子的瞬间,设线没有断裂,则下列说法不正确的是( )
处有一钉子P,把细线沿水平方向拉直,无初速度地释放小球,当细线碰到钉子的瞬间,设线没有断裂,则下列说法不正确的是( )

| A.小球的角速度突然增大 |
| B.小球的瞬时线速度突然增大 |
| C.小球的向心加速度突然增大 |
| D.小球对悬线的拉力突然增大 |
计算机硬盘内部结构如图所示,读写磁头在计算机的指令下移动到某个位置,硬盘盘面在电机的带动下高速旋转,通过读写磁头读写下方磁盘上的数据.磁盘上分为若干个同心环状的磁道,每个磁道按圆心角等分为18个扇区.现在普通的家用电脑中的硬盘的转速通常有5400r/min和7200r/min两种,硬盘盘面的大小相同,则( )

| A.磁头的位置相同时,7200r/min的硬盘读写数据更快 |
| B.对于某种硬盘,磁头离盘面中心距离越远,磁头经过一个扇区所用的时间越长 |
| C.不管磁头位于何处,5400r/min的硬盘磁头经过一个扇区所用时间都相等 |
| D.5400r/min与7200r/min的硬盘盘面边缘的某点的向心加速度的大小之比为3︰4 |
竖直放置的固定绝缘光滑轨道由半径分别为R的 圆弧MN和半径为
圆弧MN和半径为 的半圆弧NP拼接而成(两端圆弧相切于N点),小球带正电,质量为
的半圆弧NP拼接而成(两端圆弧相切于N点),小球带正电,质量为 ,电荷量为
,电荷量为 ,已知将小球由M点静止释放后,它刚好能通过P点,不计空气阻力,下列说法正确的是( )
,已知将小球由M点静止释放后,它刚好能通过P点,不计空气阻力,下列说法正确的是( )

A.若加竖直向上的匀强电场E( ),则小球能通过P点 ),则小球能通过P点 |
| B.若加竖直向下的匀强电场,则小球不能通过P点 |
| C.若加垂直纸面向里的匀强磁场,则小球不能通过P点 |
| D.若加垂直纸面向外的匀强磁场,则小球不能通过P点 |
近年来我国高速铁路发展迅速,现已知某新型国产机车总质量为m,如图已知两轨间宽度为L,内外轨高度差为h,重力加速度为g,如果机车要进入半径为R的弯道,请问,该弯道处的设计速度最为适宜的是( )

A. |
B. |
C. |
D. |
一转动装置如图甲所示,两根足够长轻杆OA、OB固定在竖直轻质转轴上的O点,两轻杆与转轴间夹角均为30°,小球a、b分别套在两杆上,小环c套在转轴上,球与环质量均为m,c与a、b间均用长为L的细线相连,原长为L的轻质弹簧套在转轴上,且与轴上P点、环c相连。当装置以某一转速转动时,弹簧伸长到 ,环c静止在O处,此时弹簧弹力等于环的重力,球、环间的细线刚好拉直而无张力。弹簧始终在弹性限度内,忽略一切摩擦和空气阻力,重力加速度为g。求:
,环c静止在O处,此时弹簧弹力等于环的重力,球、环间的细线刚好拉直而无张力。弹簧始终在弹性限度内,忽略一切摩擦和空气阻力,重力加速度为g。求:
(1)细线刚好拉直而无张力时,装置转动的角速度ω1
(2)如图乙所示,该装置以角速度ω2(未知)匀速转动时,弹簧长为L/2,求此时杆对小球的弹力大小;
(3)该装置转动的角速度由ω1缓慢变化到ω2,求该过程外界对转动装置做的功。