如图所示,质量M=2 kg的滑块套在光滑的水平轨道上,质量m=1 kg的小球通过长L=0.5 m的轻质细杆与滑块上的光滑轴O连接,小球和轻杆可在竖直平面内绕O轴自由转动,开始轻杆处于水平状态,现给小球一个竖直向上的初速度v0=4 m/s,g取10 m/s2。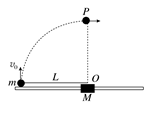
(1)若锁定滑块,试求小球通过最高点P时对轻杆的作用力大小和方向;
(2)解除对滑块的锁定,小球过最高点时速度大小v′=2 m/s,求此时滑块的速度大小。
如图所示是某次四驱车比赛的轨道某一段。小明控制的四驱车(可视为质点),质量 m=1.0kg,额定功率为P=7W。小明的四驱车到达水平平台上A点时速度很小(可视为0),此时启动四驱车的发动机并直接使发动机的功率达到额定功率,一段时间后关闭发动机。当四驱车由平台边缘 点飞出后,恰能沿竖直光滑圆弧轨道CDE上C点的切线方向飞入圆形轨道。已知AB间的距离L=6m,BF间高度差h=0.8m,圆轨道的半径R=1m,∠COD=53°,四驱车在AB段运动时的阻力恒为1N。重力加速度g取10m/s2,不计空气阻力。sin53°=0.8,cos53°=0.6,求:
点飞出后,恰能沿竖直光滑圆弧轨道CDE上C点的切线方向飞入圆形轨道。已知AB间的距离L=6m,BF间高度差h=0.8m,圆轨道的半径R=1m,∠COD=53°,四驱车在AB段运动时的阻力恒为1N。重力加速度g取10m/s2,不计空气阻力。sin53°=0.8,cos53°=0.6,求:
(1)求四驱车到达C点时的速度大小;
(2)发动机在水平平台上工作的时间;
(3)四驱车第一次经过D点时对轨道的压力大小。
如图所示,斜面轨道AB与水平面之间的夹角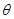 = 530,BD为半径R =" 4" m的圆弧形轨道,且B点与D点在同一水平面上,在B点,斜面轨道AB与圆弧形轨道BC在B点相切,整个轨道处于竖直平面内且处处光滑,在A点处一个质量m ="1" kg的小球由静止开始滑下,经过B、C两点后从D点斜抛出去,已知A点距地面的高度H =" 10" m,B点距地面的高度h="5" m,(不计空气阻力,g取10 m/s2,cos 530=0.6,保留两位有效数字)求:
= 530,BD为半径R =" 4" m的圆弧形轨道,且B点与D点在同一水平面上,在B点,斜面轨道AB与圆弧形轨道BC在B点相切,整个轨道处于竖直平面内且处处光滑,在A点处一个质量m ="1" kg的小球由静止开始滑下,经过B、C两点后从D点斜抛出去,已知A点距地面的高度H =" 10" m,B点距地面的高度h="5" m,(不计空气阻力,g取10 m/s2,cos 530=0.6,保留两位有效数字)求: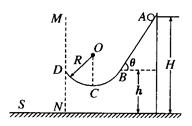
(1)小球从D点抛出后,落到水平地面上的速度;
(2)小球经过AB段所用的时间;
(3)小球经过圆弧轨道最低处C点时对轨道的压力多大?
如图所示,质量m=1 kg的小球从距离地面高H=3m处自由下落,到达地面时恰能沿凹陷于地面的半圆形槽壁运动,半圆形槽的半径R=0.5 m,小球到达槽最低点时速率恰好为8m/s,并继续沿槽壁运动直到从槽左端边缘飞出且沿竖直方向上升、下落,如此反复几次,设摩擦力大小恒定不变,取g=10 m/s2,求:
(1)小球第一次飞出半圆形槽上升到距水平地面的高度h为多少?
(2)小球最多能飞出槽外几次?
如图所示,半径R=0.4 m的光滑圆弧轨道BC固定在竖直平面内,轨道的上端点B和圆心O的连线与水平方向的夹角θ=30°,下端点C为轨道的最低点且与粗糙水平面相切,一根轻质弹簧的右端固定在竖直挡板上.质量m=0.1 kg的小物块(可视为质点)从空中A点以v0=2 m/s的速度被水平抛出,恰好从B点沿轨道切线方向进入轨道,经过C点后沿水平面向右运动至D点时,弹簧被压缩至最短,C、D两点间的水平距离L=1.2 m,小物块与水平面间的动摩擦因数μ=0.5,g取10 m/s2.求:
(1)小物块经过圆弧轨道上B点时速度vB的大小;
(2)小物块经过圆弧轨道上C点时对轨道的压力大小;
(3)弹簧的弹性势能的最大值Epm.
如图所示,在水平向右的匀强电场中,一根长为L的绝缘细线,一端连着一质量为m、带电量为+q的小球,另一端固定于O点,现把小球向右拉至细线水平且与场强方向平行的位置,无初速释放,小球能摆到最低点的另一侧,细线与竖直方向的最大夹角θ=30°.求:
(1)求场强E的大小;
(2)若使带电小球在平行于电场的竖直平面内做完整的圆周运动,小球运动过程中的最小动能是多少?
(3)若把该小球向左拉至细线水平且与场强方向平行的位置,无初速释放,小球摆到最低点时细线的拉力T=?
如图,在水平向右的匀强电场中有一固定点O,用一根长度L=0.4m的绝缘细线把质量m =0.1kg、电量q =7.5×10-5C的带正电小球悬挂在O点,小球静止在B点时细线与竖直方向的夹角为θ=37º,现将小球拉至位置A使细线水平后由静止释放,g取10m/s2.求:

(1)匀强电场的场强大小;
(2)小球运动通过最低点C时的速度大小;
(3)小球通过最低点C时细线对小球的拉力大小。
如图所示,粗糙水平面与半径R=1.5m的光滑1/4圆弧轨道相切于B点,静止于A处m =1kg的物体在大小为10N方向与水平水平面成37°角的拉力F作用下沿水平面运动,到达B点时立刻撤去F,物体沿光滑圆弧向上冲并越过C点,然后返回经过B处的速度vB=15m/s.已知SAB =15m,g=10m/s2,sin37°=0.6,cos37°=0.8。求:
(1)物体到达C点时对轨道的压力;
(2)物体与水平面的动摩擦因数μ。
某兴趣小组为了研究过山车原理,做了一个简易实验:取一段长度 1 m水平粗糙轨道
1 m水平粗糙轨道 ,如图所示,在
,如图所示,在 点设计一个竖直平面内的光滑圆轨道,半径
点设计一个竖直平面内的光滑圆轨道,半径 的大小可以调节.现有一电动小车(可视为质点)质量为
的大小可以调节.现有一电动小车(可视为质点)质量为 0.2kg静止在
0.2kg静止在 点, 通过遥控器打开电源开关,在恒定牵引力
点, 通过遥控器打开电源开关,在恒定牵引力 2N作用下开始向
2N作用下开始向 运动,小车与水平轨道的动摩擦因数为
运动,小车与水平轨道的动摩擦因数为 0.1,当小车刚好到达
0.1,当小车刚好到达 时立即关闭电源,然后进入圆轨道,
时立即关闭电源,然后进入圆轨道, =10m/s2,求:
=10m/s2,求:
(1)若圆轨道半径 =0.1m,小车到达轨道最高
=0.1m,小车到达轨道最高 点时对轨道的压力;
点时对轨道的压力;
(2)要使小车不脱离轨道,则圆轨道的半径 应满足什么条件?
应满足什么条件?
水平光滑轴上用长 的轻绳静止悬挂一小球,质量为
的轻绳静止悬挂一小球,质量为 ,
, 时刻,对小球施加一瞬时水平向右的冲击后获得动能
时刻,对小球施加一瞬时水平向右的冲击后获得动能 ,小球运动后,在最低点时再次给小球施加一与第一次同方向的瞬时冲击后获得动能,小球才恰好能到达最高点。已知小球运动中绳子始终没有弯曲。求:
,小球运动后,在最低点时再次给小球施加一与第一次同方向的瞬时冲击后获得动能,小球才恰好能到达最高点。已知小球运动中绳子始终没有弯曲。求:
(1)小球受到第二次冲击后瞬间的速度?
(2)两次冲击外力分别对小球做功的比值 的最大值?
的最大值?
某水上游乐场举办了一场趣味水上比赛.如图所示,质量m=60kg的参赛者(可视为质点),在河岸上A点紧握一根长L=5.0m的不可伸长的轻绳,轻绳另一端系在距离水面高H=10.0m的O点,此时轻绳与竖直方向的夹角为θ=37°,C点是位于O点正下方水面上的一点,距离C点x=5.0m处的D点固定着一只救生圈,O、A、C、D各点均在同一竖直面内,若参赛者抓紧绳端点,从台阶上A点沿垂直于轻绳斜向下以一定的初速度跃出,当摆到O点正下方的B点时松开手,此后恰能落在救生圈内.(sin37°=0.6,cos37°=0.8, g=10m/s2)
(1)求参赛者经过B点时速度的大小v;
(2)求参赛者从台阶上A点跃出时的动能EK;
(3)若手与绳之间的动摩擦因数为0.6,参赛者要顺利完成比赛,则每只手对绳的最大握力不得小于多少?(设最大静摩擦等于滑动摩擦力)
城市中为了解决交通问题,修建了许多立交桥,如图所示,桥面为圆弧形的立交桥AB,横跨在水平路面上,长为L=200m,桥高h=20m。可以认为桥的两端A、B与水平路面的连接处是平滑的。一辆小汽车的质量m=1040kg,以25m/s的速度冲上圆弧形的立交桥,假设小汽车冲上立交桥后就立即关闭发动机,不计车受到的摩擦阻力。试计算:(g取10m/s2)
(1)小汽车冲上桥顶时的速度是多大?
(2)小汽车在桥顶处对桥面的压力的大小。
(创编)如图所示,质量为m、电量为-q的小球,可在半径为R的固定半圆形光滑的绝缘轨道两端点M,N之间来回滚动,磁场磁感强度B垂直于轨道平面,小球在M、N处速度为零。若小球在最低点的最小压力为零,那么磁感强度B为多大?小球对轨道最低点的最大压力为多大?
(已知重力加速度为g)
如图所示,在竖直向下的匀强电场中有一带电量为q=-2×10-5C的小球,自倾角为θ=37°的绝缘斜面顶端A点由静止开始滑下,接着通过半径为R=0.5m的绝缘半圆轨道最高点C,已知小球质量为m=0.5kg,匀强电场的场强E=2×105N/C,小球运动过程中摩擦阻力及空气阻力不计,求: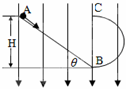
(1)H至少应为多少?
(2)通过调整释放高度使小球到达C点的速度为2m/s,则小球落回到斜面时的动能是多少?
如图所示一宇航员站在一星球表面,用一根细绳一端固定在O点,另一端固定质量为m的小球,在最低点给小球某一速度让小球在竖直平面内做完整圆周运动,小球运动到最低点和最高点绳的拉力差为F,已知该星球的半径为R,万有引力常量为G。求该星球的质量M。