高中物理探究单摆的周期与摆长的关系实验题

某同学在做“利用单摆测重力加速度”的实验中，先测得摆线长为101.00cm，摆球直径为2.00cm，然后用秒表记录了单摆振动50次所用的时间为101.5 s。则：
（1）他测得的重力加速度g =          m/s².（计算结果取三位有效数字）
(2) 他测得的g值偏小，可能原因是：          

A．测摆线长时摆线拉得过紧。

B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了。

C．开始计时时，秒表过迟按下。

D．实验中误将49次全振动计为50次。

（3）为了提高实验精度，在实验中可改变几次摆长l并测出相应的周期T，从而得出一组对应的l和T的数值，再以l为横坐标、T²为纵坐标将所得数据连成直线，并求得该直线的斜率K。则重力加速度g =          。（用K表示）

（1）某同学在做“利用单摆测重力加速度”的实验时，有下列步骤，其中正确的是
（不定项）
A．取长度约1m的细线，一端固定在铁架台上，另一端栓一个小铁球
B．测出细线的长度即为单摆的摆长L
C．使小铁球离开其平衡位置约30cm的距离，将其静止释放
D．待小铁球摆动稳定后，当小铁球经过平衡位置时按下秒表开始计时
E．开始计时时记为1，当小铁球第50次经过平衡位置停止计时，所测时间为50个周期（t=50T）
（2）若某次测量时间结果如图所示，则秒表的读数是

（3）若测出的g值较当地重力加速度的值偏大，可能原因是        （不定项）
A．小球的质量偏大
B．用摆线的长度当作摆长
C．将实际振动n次数误记为（n+1）次
D．摆线上端没有系牢，摆动过程因松动而使摆线变长           s。               

如图为用单摆测重力加速度的实验

（1）（多选题）为了减小误差，下列措施正确的是

A．摆线长度L应为线长与摆球半径的和，且在20 cm左右

B．在摆线上端的悬点处，用开有夹缝的橡皮塞夹牢摆线

C．在铁架台的竖直杆上固定一个标志物，且尽量使标志物靠近摆线

D．计时起终点都应在摆球的最高点且不少于30次全振动的时间

（2）某同学正确操作，得到了摆长L和 n次全振动的时间t，由此可知这个单摆的周期T=________；当地的重力加速度g=____________。

某同学利用如图所示的装置测量当地的重力加速度。实验步骤如下：

A．按装置图安装好实验装置；
B．用游标卡尺测量小球的直径d；
C．用米尺测量悬线的长度；
D．让小球在竖直平面内小角度摆动。当小球经过最低点时开始计时，
并计数为0，此后小球每经过最低点一次，依次计数1、2、3……。
当数到20时，停止计时，测得时间为t；
E．多次改变悬线长度，对应每个悬线长度，都重复实验步骤C、D；
F．计算出每个悬线长度对应的t ²；
G．以t ²为纵坐标、为横坐标，作出t ²－图线。
结合上述实验，完成下列任务：
（1）用游标为10分度的游标卡尺测量小球的直径。某次测量的示数如下图所示，读出小球直径d的值为          cm。

（2）该同学根据实验数据，利用计算机作出t ²–图线如图所示。根据图线拟合得到方程
t ²＝404.0 ＋3.0。由此可以得出当地的重力加速度g＝          m/s²。
（取π ² ＝ 9.86，结果保留3位有效数字）

（3）从理论上分析图线没有过坐标原点的原因，下列分析正确的是 （     ）
A．不应在小球经过最低点时开始计时，应该在小球运动到最高点开始计时；
B．开始计时后，不应记录小球经过最低点的次数，而应记录小球做全振动的次数；
C．不应作t ² –图线，而应作t –图线；
D．不应作t ² –图线，而应作t ² –（+d）图线。

某同学在做“利用单摆测重力加速度”实验中，先测得摆线长为97.20cm；用20分度的游标卡尺测小球直径如图4所示，然后用秒表记录了单摆全振动50次所用的时间为100.0s．则

（1）记录时间应从摆球经过_______________开始计时，小球直径为___________cm， 测得重力加速度g值为             m/s²（保留小数点后两位有效数字）
（2）如果他在实验中误将49次全振动数为50次，测得的g值         (填“偏大”或“偏小”或“准确”）
（3）如果该同学在测摆长时忘记了加摆球的半径，则测量结果         (填“偏大”或“偏小”或“准确”）；但是他以摆长（l）为纵坐标、周期的二次方（T²）为横坐标作出了l－T²图线，由图象测得的图线的斜率为k，则测得的重力加速度g=         。（用字母表示即可）。此时他用图线法求得的重力加速度       。（选填“偏大”，“偏小”或“准确”）

（1）在利用单摆测定重力加速度的实验中，若测得的g值偏大，可能的原因是（   ）
A．摆球质量过大
B．单摆振动时振幅较小
C．测量摆长时，只考虑了线长，忽略了小球的半径
D．测量周期时，把n个全振动误认为（n+1）个全振动，使周期偏小
（2）在演示简谐运动图象的沙摆实验中，使木板沿直线OO′做匀加速直线运动，摆动着的漏斗中漏出的沙在木板上显示出如图乙所示曲线，A．B．C．D均为直线OO′上的点，测出 ="16" cm,="48" cm，摆长为64 cm（可视为不变），摆角小于5°，则该沙摆的周期为______s，木板的加速度大小约为______ m/s2（g取10m/s2）

在《用单摆测定重力加速度》的实验中：
（1）某同学用秒表测得单摆完成40次全振动的时间如图(a)所示，则单摆的周期为       s。

（2）实验中对提高测量结果精度有利的建议是______。

A．单摆的摆线不能太短

B．单摆的摆球密度尽可能大

C．单摆的摆角越大越好

D．从平衡位置开始计时，测量一次全振动的时间作为摆动周期

（3）若单摆在任意摆角θ时的周期公式可近似为T=T₀[1+asin²(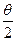)]，式中T₀为摆角趋近于0°时的周期，a为常数；为了用图象法验证该关系式，需要测量的物理量有________；某同学在实验中得到了如图(b)所示的图线，则图线的斜率表示_______。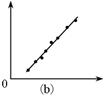

利用单摆测重力加速度的实验中，如果偏角足够小，但测出的重力加速度的数值偏大，可能原因是                                        （   ）

A．振幅较小

B．测摆长时，只量出摆线的长度，没有从悬挂点量到摆球中心

C．数振动次数时，少计了一次

D．数振动次数时，多计了一次

某兴趣小组想要探究单摆的周期T与摆长、摆球质量m的关系：
（1）为了探究周期T与摆长、摆球质量m的关系，应利用_________法完成此实验；为了准确测量单摆的周期，应使摆球振动稳定后且经过_________位置开始计时。
（2）他们在探究周期T与摆长的关系时，测得如下5组数据，请在图中选择恰当坐标，作出直观反映周期T与摆长关系的图像。

数值   　　　　次数 项目	1	2	3	4	5
	1.78	1.90	1.99	2.10	2.19
（）	3.19	3.60	3.99	4.40	4.79
（）	0.80	0.90	1.00	1.10	1.20
（）	0.64	0.81	1.00	1.21	1.44

（3）根据图像求得当地的重力加速度g=___________m/s²。（保留三位有效数字）
（4）某学生做实验时固定好装置后先测摆长，然后测出周期，发现测得的重力加速度偏大，原因可能是______（填选项前字母）

A．单摆的悬点未固定紧，振动中出现松动，使摆线增长了

B．把摆球n次经过最低点的时间误记为(n + 1)次经过最低点的时间

C．计时结束时，秒表过早按下

D．单摆所用摆球质量过大

（1）某同学在做“利用单摆测重力加速度”实验中，先测得摆线长为97.50cm；摆球直径为2.00 cm；然后用秒表记录了单摆振动50次所用的时间为99.9s．则
①该摆摆长为_______cm，周期为       s
②如果他测得的g值偏小，可能的原因是 [   ]

A．测摆线长时摆线拉得过紧
B．摆线上端未牢固地系于悬点，振动中出现松动，使摆线长度增加了
C．开始计时，秒表过迟按下	D．实验中误将49次全振动数为50次

（2）在一次用单摆测定加速度的实验中，图A的O点是摆线的悬挂点，a、b点分别是球的上沿和球心，摆长L=      m. 秒表读数__________
为了提高测量精度,需多次改变L的值并测得相应的T值.现测得的六组数据标示在以L为横坐标、T²为纵坐标的坐标纸上,即图中用“”表示的点。根据图中的数据点作出T²与L的关系图线.

用单摆测重力加速度时
（1）摆球应采用直径较小,密度尽可能_____的球,摆线长度要在1米以上,用细而不易______的尼龙线；
（2）摆线偏离竖直方向的角度θ应_______；
（3）要在摆球通过________位置时开始计时,摆线每经过此位置______次才完成一次全振动；
（4）摆球应在________面内摆动,每次计时时间内,摆球完成全振动次数一般选为___      ____次。利用单摆测重力加速度的实验中，摆长的测量应在摆球自然下垂的状况下从悬点量至                。某同学组装了如图所示的单摆，并用图示的L作为摆长，这样测得的g值将偏     。（填“大”或“小”）

有人说矿区的重力加速度偏大，某兴趣小组用单摆测定重力加速度的实验探究该问题。（1）用刻度尺测得摆长为，测量周期时用到了秒表，长针转一周的时间为30s，表盘上部的小圆共15大格，每一大格为1min，该单摆摆动n=50次时，长短针的位置如图所示，所用时间为t=________s。



（2）用以上直接测量的物理量的英文符号表示重力加速度的计算式为g=__________（不必代入具体数据）。
（3）若有一位同学在实验时测出多组单摆的摆长l和运动周期T，作出T²—图象，就可以求出矿区的重力加速度.理论上T²—图象是一条过坐标原点的直线，该同学根据实验数据作出的图象如图所示.
①造成图象不过坐标原点的原因最有可能是___________。
②由图象求出的重力加速度g＝_______m/s²（取π²=9.87）。

有一秒摆T="2" s，摆球的质量为0.04 kg，当摆球质量增加到0.08 kg时，它的周期是_______，当摆长增加到原来的4倍时，它的振动频率是_________。

一个秒摆摆球的质量为0.2 kg，它振动到最大位移时距最低点的高度为0.4 cm，它完成10次全振动回到最大位移时，距最低点的高度变为0.3 cm，如果每完成10次全振动给它补充一次能量，使摆球回到原来的高度，在60 s内总共补充的能量是____________________.

在“用单摆测定重力加速度”的实验中，用刻度尺测量悬点到小球的距离为96.60 cm，用卡尺量得小球直径是5.260 cm，测量周期有3次，每次是在摆球通过最低点时，按下秒表开始计时，同时将此次通过最低点作为第一次，接着一直数到计时终止，结果如下表.

	1	2	3
数的次数	61	81	71
时间（s）	60.40	79.80	70.60

这个单摆振动周期的测定值是_______________s，当地重力加速度的值是__________m/s².（取三位有效数字）