如图所示,斜面倾角为45°,从斜面上方A点处由静止释放一个质量为m的弹性小球,在B点处和斜面碰撞,碰撞后速度大小不变,方向变为水平,经过一段时间在C点再次与斜面碰撞。已知AB两点的高度差为h,重力加速度为g,不考虑空气阻力。求:
(1)小球在AB段运动过程中重力做功的平均功率P;
(2)小球落到C点时速度的大小。
汽车发动机的额定功率为40KW,质量为2000kg,当汽车在水平路面上行驶时受到阻力为车重的0.1倍( ),求:
),求:
(1)汽车在路面上能达到的最大速度?
(2)若汽车以额定功率启动,当汽车速度为10m/s时的加速度?
(3)若汽车从静止开始保持1m/s2的加速度作匀加速直线运动,达到额定输出功率后,汽车保持功率不变又加速行驶了800m,直到获得最大速度后才匀速行驶。求汽车从静止到获得最大行驶速度所用的总时间?
环保汽车将为2008年奥运会场馆服务。某辆以蓄电池为驱动能源的环保汽车,总质量。当它在水平路面上以
的速度匀速行驶时,驱动电机的输入电流
,电压
。在此行驶状态下
(1)求驱动电机的输入功率;
(2)若驱动电机能够将输入功率的90%转化为用于牵引汽车前进的机械功率,求汽车所受阻力与车重的比值(
);
(3)设想改用太阳能电池给该车供电,其他条件不变,求所需的太阳能电池板的最小面积。结合计算结果,简述你对该设想的思考。
已知太阳辐射的总功率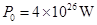 ,太阳到地球的距离
,太阳到地球的距离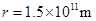 ,太阳光传播到达地面的过程中大约有30%的能量损耗,该车所用太阳能电池的能量转化效率约为15%。
,太阳光传播到达地面的过程中大约有30%的能量损耗,该车所用太阳能电池的能量转化效率约为15%。
【改编】如图所示,遥控赛车比赛中的一个规定项目是“飞跃壕沟”,比赛要求是:赛车从起点出发,沿水平直轨道运动,在B点飞出后越过“壕沟”,落在平台EF段.已知赛车的额定功率P=12.0W,赛车的质量m=1.0kg,在水平直轨道上受到的阻力f=2.0N,若比赛中赛车以额定功率运动,经过A点时速度vA=1m/s,AB段长L=10.0m,B、E两点的高度差h=1.25m,BE的水平距离x=1.5m.赛车车长不计,空气阻力不计.g取10m/s2.
(1)要使赛车越过壕沟,求赛车在B点速度至少多大;
(2)求赛车在A点时加速度大小.
(3)求赛车从A点运动到平台EF的时间
消防车的供水系统主要由水泵、输水管道和水枪组成。如图所示,消防水枪离地高度为H,建筑物上的火点A距地面高为h=60m,水枪与火点的水平距离为x,水泵的功率为P,整个供水系统的效率η=0.6。假设水从水枪水平射出,不计空气阻力,取g=10m/s2。

(1)若H=80m,水枪出水速度v0=30m/s,水枪每秒出水量m0="60" kg,水枪正中起火点A,求水泵的功率P;
(2)当完成高层灭火后,还需要对散落在火点正下方地面上的燃烧物进行灭火,将水枪竖直下移至H´=45m,假设供水系统的效率η不变,水枪出水口的横截面积不变,水泵功率应调整为P´,则P´应为多大?
洋流又叫海流,指大洋表层海水常年大规模的沿一定方向较为稳定的流动。因为海水中含有大量的正、负离子,这些离子随海流做定向运动,如果有足够强的磁场能使海流中的正、负离子发生偏转,便可用来发电。图为利用海流发电的磁流体发电机原理示意图,其中的发电管道是长为L、宽为d、高为h的矩形水平管道。发电管道的上、下两面是绝缘板,南、北两侧面M、N是电阻可忽略的导体板。两导体板与开关S和定值电阻R相连。整个管道置于方向竖直向上、磁感应强度大小为B的匀强磁场中。为了简化问题,可以认为:开关闭合前后,海水在发电管道内以恒定速率v朝正东方向流动,发电管道相当于电源,M、N两端相当于电源的正、负极,发电管道内海水的电阻为r(可视为电源内阻)。管道内海水所受的摩擦阻力保持不变,大小为f。不计地磁场的影响。
(1)判断M、N两端哪端是电源的正极,并求出此发电装置产生的电动势;
(2)要保证发电管道中的海水以恒定的速度流动,发电管道进、出口两端要保持一定的压力差。请推导当开关闭合后,发电管两端压力差F与发电管道中海水的流速v之间的关系;
(3)发电管道进、出口两端压力差F的功率可视为该发电机的输入功率,定值电阻R消耗的电功率与输入功率的比值可定义为该发电机的效率。求开关闭合后,该发电机的效率η;在发电管道形状确定、海水的电阻r、外电阻R和管道内海水所受的摩擦阻力f保持不变的情况下,要提高该发电机的效率,简述可采取的措施。
某兴趣小组对遥控车的性能进行研究。他们让小车在平直轨道上由静止开始运动,并将运动的全过程记录下来并得到v-t图象,如图所示,除2s-10s内的图线为曲线外,其余均为直线,已知小车运动的过程中,2s—14s内小车的功率保持不变,在第14s末关闭动力让小车自由滑行,已知小车的质量为1kg,可认为在整个过程中小车所受到的阻力大小不变。求:
(1)小车匀速行驶阶段的功率;
(2)小车在第2-10s内位移的大小。
如图甲所示是一打桩机的简易模型.质量m=1kg的物体在恒定拉力F作用下从与钉子接触处由静止开始运动,上升一段高度后撤去F,到最高点后自由下落,撞击钉子,将钉子打入一定深度.物体上升过程中,机械能E与上升高度h的关系图像如图乙所示.不计所有摩擦,g取10m/s2.求:
(1)物体上升到1m高度处的速度;
(2)物体上升1 m后再经多长时间才撞击钉子(结果可保留根号);
(3)物体上升到0.25m高度处拉力F的瞬时功率.
动车组是城际间实现小编组、大密度的高效运输工具,以其编组灵活、方便、快捷、安全、可靠、舒适等特点而备受世界各国铁路运输和城市轨道交通运输的青睐.动车组就是几节自带动力的车厢加几节不带动力的车厢编成一组,就是动车组.假设有一动车组由8节车厢连接而成,每节车厢的总质量均为7.5×104 kg.其中第一节、第二节带动力,他们的额定功率均为3.6×107W和2.4×107W,车在行驶过程中阻力恒为重力的0.1倍(g =10m/s2)
(1)求该动车组只开动第一节的动力的情况下能达到的最大速度;
(2)若列车从A地沿直线开往B地,先以恒定的功率6×107W(同时开动第一、第二节的动力)从静止开始启动,达到最大速度后匀速行驶,最后除去动力,列车在阻力作用下匀减速至B地恰好速度为0.已知AB间距为5.0×104m,求列车从A地到B地的总时间.
在许多建筑工地经常使用打夯机将桩料打入泥土中以加固地基。打夯前先将桩料扶起、使其缓慢直立进入泥土中,每次卷扬机都通过滑轮用轻质钢丝绳将夯锤提升到距离桩顶 =5m处再释放,让夯锤自由下落,夯锤砸在桩料上并不弹起,而随桩料一起向下运动。设夯锤和桩料的质量均为m="500" kg,泥土对桩料的阻力为
=5m处再释放,让夯锤自由下落,夯锤砸在桩料上并不弹起,而随桩料一起向下运动。设夯锤和桩料的质量均为m="500" kg,泥土对桩料的阻力为 ,其中常数
,其中常数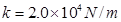 ,
, 是桩料深入泥土的深度。卷扬机使用电动机来驱动,卷扬机和电动机总的工作效率为
是桩料深入泥土的深度。卷扬机使用电动机来驱动,卷扬机和电动机总的工作效率为 =95%,每次卷扬机需用20 s的时间提升夯锤。提升夯锤时忽略加速和减速的过程,不计夯锤提升时的动能,也不计滑轮的摩擦。夯锤和桩料的作用时间极短,g取10
=95%,每次卷扬机需用20 s的时间提升夯锤。提升夯锤时忽略加速和减速的过程,不计夯锤提升时的动能,也不计滑轮的摩擦。夯锤和桩料的作用时间极短,g取10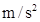 ,求:
,求: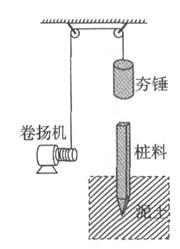
(1)在提升夯锤的过程中,电动机的输入功率;(结果保留2位有效数字)
(2)打完第一夯后,桩料进入泥土的深度。
某同学利用玩具电动车模拟腾跃运动。如图所示,AB是水平地面,长度为L=6m,BCDE是一段曲面,且在B点处平滑连接。玩具电动车的功率始终为P=10W,从A点由静止出发,到达离地面h=1.8m的E点水平飞出,落地点与E点的水平距离x=2.4m。玩具电动车可视为质点,总质量为m=1kg,重力加速度g取10m/s2,不计空气阻力。求:
(1)玩具电动车过E点时的速度;
(2)若玩具电动车在AB段所受的阻力Ff恒为2N,从B点到E点的过程中,克服摩擦阻力做功10J,则从A点至E点过程所需要的时间是多少?
如图甲所示,光滑且足够长的平行金属导轨MN、PQ固定在同一水平面上,两导轨间距L=0.30m。导轨电阻忽略不计,其间接有固定电阻R=0.40Ω.导轨上停放一质量为m=0.10kg、电阻r=0.20Ω的金属杆ab,整个装置处于磁感应强度B=0.50T的匀强磁场中,磁场方向竖直向下。利用一外力F沿水平方向拉金属杆ab,使之由静止开始做匀加速直线运动,电压传感器可将R两端的电压U即时采集并输入电脑,并获得U随时间t的关系如图乙所示。求:
(1)金属杆加速度的大小;
(2)第2s末外力的瞬时功率。
如图所示,在冬奥会上,跳台滑雪运动员从滑道上的A点由静止滑下,经时间t0从跳台末端的O点沿水平方向飞出。O点又是斜坡OB的起点,A点与O点在竖直方向的高度差为h,斜坡OB的倾角为θ。运动员的质量为m,重力加速度为g。不计一切摩擦和空气阻力。求:
⑴从A点到O点的运动过程中,重力对运动员做功的平均功率;
⑵运动员在斜坡OB上的落点到O点的距离S;
⑶若运动员在空中飞行时处理好滑雪板和水平面的夹角,便可获得一定的竖直向上的升力。假设该升力为运动员全重的5﹪,求实际落点到O点的距离将比第⑵问求得的距离远百分之几?(保留三位有效数字)
如图,水平轨道AB与竖直固定圆轨道相切于B点,C为圆轨道最高点,圆轨道半径R=5m.一质量m=60kg的志愿者,驾驶质量M=940kg、额定功率P=40kW的汽 车体验通过圆轨道时所受底座的作用力,汽车从A点由静止以加速度a=2m/s2做匀 加速运动,到达B点时,志愿者调节汽车牵引力,使汽车匀速率通过圆轨道又回到B点,志愿者在C点时所受底座的支持力等于志愿者的重力,已知汽车在水平轨道及圆轨道上的阻力均为汽车对轨道压力的0.1倍,取g=10m/s2,计算中将汽车视为质点。
求:
(1)汽车在C点的速率;
(2)汽车在C点的牵引功率;
(3)AB间的距离及汽车从A点经圆轨道又回到B点的过程所用的时间。
如图所示,长L=9m的传送带与水平方向的倾角为37°,在电动机的带动下以v="4m/s" 的速率顺时针方向运行,在传送带的B端有一离传送带很近的挡板P可将传送带上的物块挡住,在传送带的A端无初速地放一质量m=1kg的物块,它与传送带间的动摩擦因数 =0.5,物块与挡板的碰撞能量损失及碰撞时间不计。(sinθ=0.6,cosθ=0.8,g=10m/s2)问:
=0.5,物块与挡板的碰撞能量损失及碰撞时间不计。(sinθ=0.6,cosθ=0.8,g=10m/s2)问:
(1)物块与挡板P第一次碰撞后,上升到最高点时到挡板P的距离;
(2)若改为将一与皮带间动摩擦因素为μ=0.875、质量不变的新木块轻放在B端,求木块运动到A点过程中电动机多消耗的电能与电动机额定功率的最小值。