高中物理验证牛顿第二运动定律计算题

如下图所示，质量为40.0kg的雪橇（包括人）在与水平方向成37°角、大小为200N的拉力F作用下，沿水平面由静止开始运动，雪橇与地面间动摩擦因数为0.20；取g=10m/s²，cos37°=0.8，sin37°=0.6。
求雪橇的加速度大小；
经过2s撤去F，再经过3s时雪橇的速度多大？
雪橇在5s内的位移多大？

有些国家的交管部门为了交通安全，特制定了死亡加速度为500g(g＝10 m/s²)这一数值以警示世人．意思是如果行车加速度超过此值，将有生命危险．这么大的加速度，一般车辆是达不到的，但是如果发生交通事故时，将会达到这一数值．试判断：
两辆摩托车以36 km/h的速度相向而撞，碰撞时间为2×10^－3 s，驾驶员是否有生命危险？

如图，一块质量为M = 2kg，长L = 1m的匀质木板放在足够长的光滑水平桌面上，初始时速度为零．板的最左端放置一个质量m = 1kg的小物块，小物块与木板间的动摩擦因数为μ = 0.2，小物块上连接一根足够长的水平轻质细绳，细绳跨过位于桌面边缘的定滑轮（细绳与滑轮间的摩擦不计，木板与滑轮之间距离足够长，g = 10m/s²）。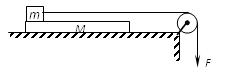

若木板被固定，某人以F= 4N向下拉绳，则小木块滑离木板所需要的时间是多少？
整个过程恒力F做多少功？
若木板不固定，某人仍以恒力F = 4N向下拉绳，则小木块滑离木板所需要的时间是多少？整个过程恒力F做多少功？

滑板运动是利用汽艇牵引运动员在水上滑行的一种运动（如图所示），滑行时汽艇用一根直径为6.3cm，长23m的拖索拖拉，且拖索头上装有一根直径为25cm-28cm的木质握把供滑水运动员握持。设一个质量为M=70kg的运动员，使用一个质量为m=10kg下面接近平面的滑板滑水，若带动运动员的汽艇以其额定功率P=21KW水平拉着运动员以速度v=108km/h做匀速运动，设在运动过程中汽艇受到空气和水的阻力恒为f₁=60N，人和滑板受到的各种水平阻力恒为f₂=40N，则

1）运动员脚下滑板与竖直方向的夹角应为多大？
2）如果该汽艇拖着滑板和人仍使其以原来的速度大小开始做半径为R=90m的匀速圆周运动，设拖索的拉力和阻力方向接近于切线方向，则滑水运动员应如何调整滑板与竖直方向的夹角？

质量为4kg的雪橇在倾角=37°的足够长斜坡上向下滑动，所受的空气阻力与速度成正比，比例系数K未知，今测得雪橇运动的v—t图象如图曲线AD所示，且AB是曲线最左端A点的切线，B点的坐标为（4，15），平行于ot轴的CD线是曲线的渐近线。已知sin37°=0．6，g=l0m/s²。试问：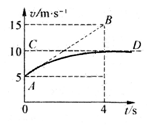

（1）物体在开始计时的一段时间里做什么性质的运动？最终做什么运动？
（2）当v_o =5m／s和v₁="10" m／s时，物体的加速度各是多少？
（3）空气阻力系数k及雪橇与斜坡间的动摩擦因数各是多少？

如图所示的装置叫做阿特伍德机，是阿特伍德创制的一种著名力学实验装置，用来研究匀变速直线运动的规律。绳子两端的物体下落（上升）的加速度总是小于自由落体的加速度g，同自由落体相比，下落相同的高度，所花费的时间要长，这使得实验者有足够的时间从容的观测、研究。已知物体A、B的质量相等均为M，物体C的质量为m，轻绳与轻滑轮间的摩擦不计，轻绳不可伸长且足够长，如果，求：

（1）物体B从静止开始下落一段距离的时间与其自由落体下落同样的距离所用时间的比值。
（2）系统在由静止释放后的运动过程中，物体C对B的拉力。

如图所示，水平传送带以一定速度匀速运动，将质量m=1kg的小物块轻轻放在传送带上的P点，物块运动到A点后被水平抛出，小物块恰好无碰撞地沿圆弧切线从B点进入竖直光滑圆弧轨道下滑．B、C为圆弧上的两点，其连线水平，已知圆弧对应圆心角，A点距水平面的高度h=0.8m．小物块到达C点时的速度大小与B点相等，并沿固定斜面向上滑动，小物块从C点到第二次经过D点的时间间隔为0.8s，已知小物块与斜面间的动摩擦因数，重力加速度g取10 m/s²，取，cos53°=0.6，求：

（1）小物块从A到B的运动时间；
（2）小物块离开A点时的水平速度大小；
（3）斜面上C、D点间的距离．

一机动车拉一拖车，由静止开始在水平轨道上匀加速前进，在运动开始后的头10s内走过40m，然后将拖车解脱．但机车的牵引力仍旧不变，再过10s两车相距60m．试求机动车和拖车质量之比．（计算时一切阻力均不计）

如图所示，半径R=0.8m的光滑圆弧MN竖直放置，M为圆弧最高点，N为圆弧最低点且与水平粗糙地面平滑连接。现有一物块A从M点由静止释放，最后在水平上面滑行了4m停止。物块A可视为质点，取g= 10m/s²₊，则：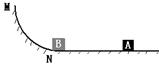

（1）物块A刚滑到N点的加速度与刚滑过N点的加速度大小之比。
（2）若物块A以一定的初动能从M点下滑，一段时间后另一光滑的物块B（视为质点）从M处静止释放，当B滑到N处时，A恰好在B前方x=7m处，且速度大小为10m/s，则B再经过多少时间可追上A？

如图所示的装置叫做阿特伍德机，是阿特伍德创制的一种著名力学实验装置，用来研究匀变速直线运动的规律。绳子两端的物体下落（上升）的加速度总是小于自由落体的加速度g，同自由落体相比，下落相同的高度，所花费的时间要长，这使得实验者有足够的时间从容的观测、研究。已知物体A、B的质量相等均为M，物体C的质量为m，轻绳与轻滑轮间的摩擦不计，轻绳不可伸长且足够长，如果，求：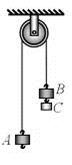

（1） 物体B从静止开始下落一段距离的时间与其自由落体下落同样的距离所用时间的比值。
（2）系统在由静止释放后的运动过程中，物体C对B的拉力。

如图4所示，A、B两物体的质量分别为m_A=2.0kg、m_B=4.0kg。 物体A与桌面间的动摩擦因数=0.2，当轻轻释放B后，求：

（1）物体A沿桌面滑行的加速度是多少？
（2）物体A受到绳子的拉力多大？（取g=10m/s²）

如图所示，在倾角θ＝37°的足够长的固定的斜面底端有一质量m＝1.0 kg的物体，物体与斜面间动摩擦因数μ＝0.25，现用轻细绳将物体由静止沿斜面向上拉动，拉力F＝10.0 N，方向平行斜面向上，经时间t₁＝4.0 s绳子突然断了，(sin37°＝0.60，cos37°＝0.80，g＝10 m/s²)求：
 
(1)绳断时物体的速度大小；
(2)从绳子断开到物体再返回到斜面底端的运动时间？

有一辆汽车的质量为2×10³kg，额定功率为9×10⁴W。汽车在平直路面上由静止开始运动，所受阻力恒为3×10³N。在开始起动的一段时间内汽车以1m/s²的加速度匀加速行驶。从开始运动到停止加速所经过的总路程为270m。求：
（1）汽车匀加速运动的时间；
（2）汽车能达到的最大速度；
（3）汽车从开始运动到停止加速所用的时间。

一物快以一定的初速度沿足够长的斜面向上滑动，其速度大小随时间的变化关系图如图所示，取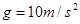，求：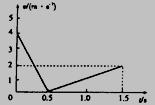

（1）物快上滑过程和下滑过程的加速度大小；
（2）物快向上滑行的最大距离；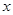
（3）斜面的倾角.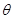

光滑的斜面倾角θ=30º，斜面底端有弹性挡板P，长2l、质量为M的两端开口的圆筒置与斜面上,下端在B点处， PB=2l，圆筒的中点处有一质量为m的活塞，M=m．活塞与圆筒壁紧密接触，最大静摩擦力与滑动摩擦力相等为f=mg/2．每当圆筒中的活塞运动到斜面上AB区间时总受到一个沿斜面向上F=mg的恒力作用，AB=l.现由静止开始从B点处释放圆筒．

（1）求活塞位于AB区间之上和进入AB区间内时活塞的加速度大小；
（2）求圆筒第一次与挡板P碰撞前的速度和经历的时间；
（3）圆筒第一次与挡板P瞬间碰撞后以原速度大小返回，求圆筒沿斜面上升到最高点的时间．