高中物理力学实验试题

如图，细杆的一端与一小球相连，可绕过O点的水平轴自由转动，现给小球一初速度，使它在竖直平面内做圆周运动，图中a、b分别表示小球轨道的最低点和最高点，则杆对球的作用力情况是（   ）

A．a处可能是压力	B．b处一定是拉力
C．b处一定是支持力	D．b处可能没有弹力

一物体做自由落体运动，在第1s末和第2s末重力做功的瞬时功率之比分别为（   ）

A．1:2

B．1:3

C．1:4

D．1:9

某同学在用单摆测重加速度的实验中，用的摆球密度不均匀，无法确定重心位置，他第一次量得悬线长为L₁（不计摆球半径），测得周期为T₁，第二次量得悬线长为L₂，测得周期为T₂，根据上述数据，重力加速度g的值为：（  ）

A．	B．
C．	D．无法判断

如图所示，质量为m的小球从空中的A点开始做自由落体运动，下降了高度h。在这一过程中，重力对小球做的功等于       ，重力对小球做功的平均功率等于       。（已知重力加速度为g）

铁路提速要解决许多技术问题，其中提高机车牵引力功率是一个重要问题。已知列匀速运动时，列车所受附图与速度的平方成正比，即。设提速前速度为，速后速度为，则提速前与提速后，机车牵引力的功率之比为                        （   ）

A．

B．

C．

D．

利用单摆测重力加速度的实验中，如果偏角足够小，但测出的重力加速度的数值偏大，可能原因是                                        （   ）

A．振幅较小

B．测摆长时，只量出摆线的长度，没有从悬挂点量到摆球中心

C．数振动次数时，少计了一次

D．数振动次数时，多计了一次

关于重心，下列说法正确的是（     ）

A．物体的重心一定在物体上

B．物体的质量全部集中在重心上

C．物体的重心位置跟物体的质量分布情况和物体的形状有关

D．物体的重心跟物体的质量分布没有关系

下列关于加速度的说法中正确的是（    ）

A．加速度表示物体运动的快慢

B．加速度表示物体速度变化的快慢

C．物体运动速度越大，其加速度越大

D．物体运动速度为零，其加速度一定也为零

一位质量m=50kg的滑雪运动员从高度h=30m的斜坡自由滑下（初速度为零）。斜坡的倾角θ=37°，滑雪板与雪面滑动摩擦因素=0.1。则运动员滑至坡底的过程中有：
（1）所受几个力所做的功各是多少？
（2）合力做了多少功？
（3）到达坡底时摩擦力的功率是多少？（不计空气阻力）

关于功率以下说法中正确的是：（　  ）     

A．据P＝W/t可知，机器做功越多，其功率就越大

B．据P＝Fv可知，汽车牵引力一定与速度成反比

C．据P＝W/t可知，只要知道在时间t内机器所做的功，就可求得这段时间内任一时刻机器做功的功率

D．根据P＝Fv可知，发动机功率一定时，汽车的牵引力与运动速度成反比

放在桌面上的台灯，对桌面有压力，其受力物体是      ，施力物体是          。

如图是某辆汽车的汽车速度计。汽车启动后经过15s速度表的 指针指在如图所示的位置。由表可知（   ）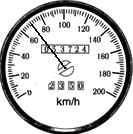

A．此时汽车的瞬时速度是70m/s

B．启动后15s内汽车的平均速度是70km/h

C．启动后15s内汽车的平均速度是70m/s

D．此时汽车的瞬时速度是70km/h

如图所示，物体A在光滑的斜面上沿斜面下滑，则A受到的作用力是(          )

A．重力、弹力和下滑力	B．重力和弹力
C．重力和下滑力	D．重力、压力和下滑力

关于加速度，下列说法不正确的是                           (        )

A．加速度的大小与速度的大小无必然联系

B．加速度的方向与速度的方向可能相同，也可能相反

C．加速度很大时物体速度可能很小

D．加速度大的物体速度变化一定很大

如图所示，AA₁为固定在竖直方向上的钢环C的竖直直径，弹簧一端固定于A点，另一端与穿在C中的小光滑环B固定，若更换不同劲度系数的弹簧B都能在 AA₁右侧静止，在这些条件下，C对B的弹力的方向和大小为：

A．大小和方向都不同

B．大小和方向都相同

C．大小相同，方向不同

D．方向相同，大小不同