高中物理力学实验计算题

如图所示,位于竖直平面上的圆弧轨道,半径为R,OB沿竖直方向,上端A距地面高度为H,质量为m的小球从A点释放,最后落在水平地面上C点处。不计空气阻力。已知小球到达B点时对圆弧轨道的压力为3mg,求:

(1)小球到达B点时的速度大小。
(2)小球在离开B点前后瞬间的加速度大小。
(3)小球落地点C与B点的水平距离s。

如图所示，一个人用一根长L=1m，只能承受T=46N拉力的绳子，拴着一个质量为m=1kg的小球，在竖直面内做逆时针方向的圆周运动，已知圆心O离地的距离H=6m，g=10m/s²。

（1）此人在小球到达最低点时必须用多大的角速度转动小球方能使绳子被拉断？
（2）若地面上P点停有一只视为质点的乌龟，P点与O点的水平距离为7米，问绳子拉断后，小球第一次着地是否会击中乌龟？如没击中，则小球第一次着地点距乌龟多远？

）一劲度系数k＝800 N/m的轻质弹簧两端分别连接着质量均为12 kg的物体A、B，将它们竖直静止放在水平面上，如图所示．现将一竖直向上的变力F作用在A上，使A开始向上做匀加速运动，经0.40 s物体B刚要离开地面．g＝10 m/s²，

试求：
(1)物体B刚要离开地面时，A物体的速度v_A；
(2)物体A重力势能的改变量；

一竖直固定光滑的半圆形轨道ACB，圆心为O，半径为R。在最高点A把小球以平抛，小球碰到轨道后不反弹（沿轨道径向速度减为0），忽略一切阻力，求：

①．小球打到轨道上D点（图中未画出）时下落的高度；
②．小球到达最低点B时速度和对轨道的压力。

一半径为圆盘可绕通过圆盘中心O且垂直于盘面的竖直轴转动,圆盘距地面的竖直高度为2R.距圆盘中心Ｒ处放一小木块，它与圆盘之间相对静止且随圆盘一起做匀速圆周运动，已知木块与圆盘之间的动摩擦因数为1/3。设木块与圆盘间的最大静摩擦力等于滑动摩擦力。

（1）求圆盘转动的最大角速度
（2）若圆盘以最大角速度转动，某时刻圆盘突然停止转动，小木块离开圆盘最后落到地面。求木块离开圆盘时的速度及落地点与圆盘中心O的水平距离。

一轻绳两端分别固定在一根竖直棒上相距为L=2.5m的A、B两点，一个质量为m=0.6kg的光滑小圆环套在绳子上，当竖直棒以一定的角速度转动时，圆环以A为圆心在水平面上作匀速圆周运动，（θ= 37°g=10m/s²）则

（1）此时轻绳上的张力大小等于多少？
（2）竖直棒转动的角速度为多大？

如图所示，重力为G₁=8N的砝码悬挂在绳PA和PB的结点上，PA偏离竖直方向37°角，PB沿水平方向且连在重力为G₂=100N的木块上，木块静止于倾角为37°的斜面上，试求：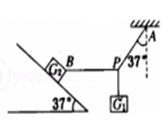

（1）PA、PB绳上的拉力分别为多大？
（2）木块与斜面间的摩擦力；
（3）木块所受斜面的弹力．

如图所示，水平轨道MN与竖直光滑半圆轨道相切于N点，轻弹簧左端固定在轨道的M点，将一质量为m=1kg的小物块靠在弹簧右端并压缩至O点，此时弹簧储有弹性势能E_p，现将小物块无初速释放，小物块恰能通过轨道最高点B，此后水平飞出再落回到水平面。已知ON的距离L=3.0m，小物块与水平轨道间的动摩擦因数μ=0.2，圆轨道半径R=0.4m，g取10 m/s²。求：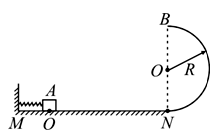

（1）小物块通过B点抛出后，落地点距N的水平距离x；
（2）弹簧储有的弹性势能E_p。

如图所示，一个质量为m的小球用一根长为l的细绳吊在天花板上，给小球一水平初速度，使它做匀速圆周运动，小球运动所在的平面是水平的。已知细绳与竖直方向的夹角为θ，重力加速度为g。求：

（1）细绳对小球的拉力；
（2）小球做圆周运动的线速度。

如图，质量为0．5kg的小杯里盛有1kg的水，用绳子系住小杯在竖直平面内做“水流星”表演，转动半径为1m，g取10m／s。求：

（1）为使小杯经过最高点时水不流出，在最高点时最小速率是多少?
（2）当水杯在最高点速率V₂=5m／s时，在最高点时，绳的拉力?

如图所示，轻线一端系一质量为m的小球，另一端套在图钉A上，此时小球在光滑的水平平台上做半径为、周期为T的匀速圆周运动。现拔掉图钉A让小球飞出，此后细绳又被A正上方距A高为h的图钉B套住，达稳定后，小球又在平台上做匀速圆周运动。求：

（1）图钉A拔掉前，轻线对小球的拉力大小。
（2）从拔掉图钉A到被图钉B套住前小球做什么运动？所用的时间为多少？
（3）小球最后做圆周运动的周期。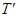

随着世界各国航天事业的发展，宇宙探测已成为各国关注的热点，宇宙中有颗类地行星，质量是地球质量的2倍，直径也是地球直径的2倍，假若发射一个质量m=5000kg的探测器对该星体表面进行勘察研究，该探测器内装有发动机，探测器软着陆在一块平地上的P点，距离着陆 的指定目标A点还有距离L=12m，探测器落地稳定后启动发动机，让探测器以a₁=1m/s²的加速 度开始作勻加速运动，到达A点前关闭发动机最后恰停在A点。已知探测器与该星体地面间 的动摩擦因数为μ=0.2，地球表面的重力加速度g=10m/s²。求：
（1）该星体表面的重力加速度为多大？
（2）探测器从P点到达A点的过程中，发动机所做的功为多少？
（3）从P点到达A点的过程中探测器的最大速度和最大功率分别为多少？

如图所示，长为R的轻质杆（质量不计），一端系一质量为m的小球（球大小不计），绕杆的另一端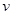在竖直平面内做圆周运动

（1）若小球最低点时，杆对球的弹力大小为5mg，则小球的向心加速度为多大？
（2）小球通过最高点时，杆与小球间的弹力大小为0.75mg,则小球的线速度为多大？

在倾角为θ的斜坡上，某同学骑在自行车上，刚好能在不踩踏板的情况下使自行车沿斜坡匀速向下行驶。现在他骑着自行车以某一速度沿此斜坡匀速上行，已知在t时间内，他踩着脚蹬板转了N圈（不间断地匀速蹬），又已知自行车和人的总质量为m，自行车链轮的半径为R₁，飞轮的半径为R₂，后车轮的半径为R₃，设上、下坡过程中斜坡及空气作用于自行车的阻力大小相等，车轮与坡面接触处都无滑动（提示：自行车行驶的速度等于后轮边缘一点相对于轴心转动的线速度大小），不计自行车内部各部件之间因相对运动而消耗的能量。求人骑自行车上坡时的功率。

如图所示，一个重为G=20N的木块放在倾角30°的光滑斜面上，被一根劲度系数k=250N/m的轻弹簧拉着．该弹簧原长l₀=0.20m，求:

(1)物体静止在斜面上时弹簧对物体的拉力F多大？
(2)此时弹簧的长度L为多少？