高中物理力学实验计算题

如图所示，是一传送装置，其中AB段粗糙，AB段长为L＝1 m，动摩擦因数μ＝0.5；BC、DEN段均可视为光滑，DEN是半径为r＝0.5 m的半圆形轨道，其直径DN沿竖直方向，C位于DN竖直线上，CD间的距离恰能让小球自由通过。其中N点又与足够长的水平传送带的右端平滑对接，传送带以6m/s的速率沿顺时针方向匀速转动，小球与传送带之间的动摩擦因数也为0.5。左端竖直墙上固定有一轻质弹簧，现用一可视为质点的小球压缩弹簧至A点后由静止释放(小球和弹簧不粘连)，小球刚好能沿圆弧DEN轨道滑下，而始终不脱离轨道。已知小球质量m＝0.2 kg ，g 取10m/s²。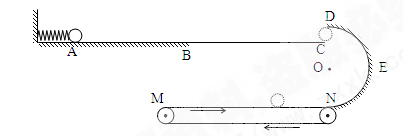

（1） 求小球到达D点时速度的大小及弹簧压缩至A点时所具有的弹性势能；
（2） 小球第一次滑上传送带后的减速过程中，在传送带上留下多长的痕迹？
（3） 如果希望小球能沿着半圆形轨道上下不断地来回运动，且始终不脱离轨道，则传送带的速度应满足什么要求？

一质量不计的弹簧原长为10 cm，一端固定于质量m＝2 kg的物体上，另一端施一水平拉力F.( ，设最大静摩擦力与滑动摩擦力相等)

(1)若物体与水平面间的动摩擦因数为0.2，当弹簧拉长至14cm时，物体恰好被拉动，弹簧的劲度系数多大？
(2)若将弹簧拉长至11 cm时（物体在滑动过程中），物体所受的摩擦力大小为多少？
(3)物体静止时，若将弹簧拉长至13cm，物体所受到的摩擦力大小为多少？

原长 l₀＝12cm的弹簧，上端固定，下端挂质量为 m＝4kg的物块， 静止时弹簧 l₁＝20cm。 当将该物块放在水平桌面上， 并用上述弹簧沿水平方向拉物块。当弹簧长度为l₂＝15cm时，物块恰好被拉动。此后为保持物块做匀速直线运动，弹簧长度维持在l₃＝14cm。(g＝10m/s²)求：

⑴弹簧的劲度系数k；
⑵物块与水平桌面之间的最大静摩擦力f_m；
⑶物块与水平面之间的动摩擦因数μ。

如图所示是利用电动机提升重物的示意图，其中D是直流电动机．P是一个质量为m的重物，它用细绳拴在电动机的轴上．闭合开关S，重物P以速度v被匀速提升，这时电流表和电压表的示数分别是I＝5.0Ａ和U＝110Ｖ，重物P上升的速度v＝0.90m/s．重物的质量ｍ＝50kg。不计一切摩擦，g取．求:

（1）电动机消耗的电功率P_电；
（2）电动机线圈的电阻R.

如图所示，竖直平面内固定着这样的装置：倾斜的粗糙细杆底端与光滑的圆轨道相接，细杆和圆轨道相切于B点，细杆的倾角为37°，长为L，半圆轨道半径为R＝0.2L。一质量为m的小球（可视为质点）套在细杆上，从细杆顶端A由静止滑下，滑至底端B刚好套在圆轨道上继续运动。球与杆间的动摩擦因数为μ=0.25， cos37°=0.8，sin37°=0.6。求：

（1）小球滑至细杆底端B时的速度大小；
（2）试分析小球能否滑至光滑竖直圆轨道的最高点C。如能，请求出在最高点时小球对轨道的压力；如不能，请说明理由；
（3）若给球以某一初速度从A处下滑，球从圆弧最高点飞出后做平抛运动 ，欲使其打到细杆上与圆心O等高的D点，求球在C处的速度大小及撞到D点时速度与水平方向夹角的正切值。                           

如图所示，用内壁光滑的薄壁细管弯成的“S”形轨道固定于竖直平面内，其弯曲部分是由两个半径均为R的半圆平滑对接而成（圆的半径远大于细管内径），轨道底端D点与粗糙的水平地面相切。现一辆玩具小车m以恒定的功率从E点由静止开始出发，经过一段时间t之后，出现了故障，发动机自动关闭，小车在水平地面继续运动并进入“S”形轨道，从轨道的最高点A飞出后，恰好垂直撞在固定斜面B上的C点，C点与下半圆的圆心等高。已知小车与地面之间的动摩擦因数为μ，ED之间的距离为x₀，斜面的倾角为30º。求：

（1）小车到达C点时的速度大小为多少?
（2）在A点小车对轨道的压力是多少，方向如何？
（3）小车的恒定功率是多少？

石墨烯是近些年发现的一种新材料，其超高强度及超强导电、导热等非凡的物理化学性质有望使21世纪的世界发生革命性的变化，其发现者由此获得2010年诺贝尔物理学奖．用石墨烯制作超级缆绳，人类搭建“太空电梯”的梦想有望在本世纪实现．科学家们设想，通过地球同步轨道站向地面垂下一条缆绳至赤道基站，电梯仓沿着这条缆绳运行，实现外太空和地球之间便捷的物资交换．

(1) 有关地球同步轨道卫星，下列表述正确的是：
A.卫星距离地面的高度大于月球离地面的高度
B.卫星的运行速度小于第一宇宙速度
C.卫星运行时可能经过嘉兴的正上方
D.卫星运行的向心加速度小于地球表面的重力加速度
(2) 若把地球视为质量分布均匀的球体，已知同步卫星绕地球做匀速圆周运动的向心加速度大小为a₁，近地卫星绕地球做匀速圆周运动的向心加速度大小为a₂,地球赤道上的物体做匀速圆周运动的向心加速度大小为a₃，地球北极地面附近的重力加速度为g₁，地球赤道地面附近的重力加速度为g₂，则：
A. a₁=g₁        B. a₂=g₁       C. a₃=g₁        D. g₁ -g₂=a₃
(3)当电梯仓停在距地面高度h＝4R的站点时，求仓内质量m＝50kg的人对水平地板的压力大小．取地面附近重力加速度g取10m/s²，地球自转角速度ω＝7.3×10^－5rad/s，地球半径R＝6.4×10³km.（结果保留三位有效数字）

一质量m＝1 kg的物体在沿斜面向上的拉力F＝12 N作用下恰能沿倾角α＝37°的斜面匀速上滑，求物体与斜面间的动摩擦因数μ。(已知cos 37°＝0.8，sin 37°＝0.6，g＝10 N/kg)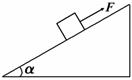

如图所示，斜面轨道AB与水平面之间的夹角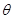= 53⁰，BD为半径R =" 4" m的圆弧形轨道，且B点与D点在同一水平面上，在B点，斜面轨道AB与圆弧形轨道BC在B点相切，整个轨道处于竖直平面内且处处光滑，在A点处有一质量m ="1" kg的小球由静止滑下，经过B、C两点后从D点斜抛出去，已知A点距地面的高度H =" 10" m，B点距地面的高度h="5" m，（不计空气阻力，g取10 m/s²，cos 53⁰=0.6，保留两位有效数字）求：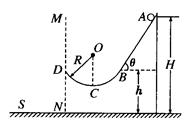

（1）小球从D点抛出后，落到水平地面上的速度
（2）小球经过AB段所用的时间？
（3） 小球经过圆弧轨道最低处C点时对轨道的压力多大？

总质量为100 kg的小车，在粗糙水平地面上从静止开始运动，其速度—时间图象如图所示。已知在0—2s时间内小车受到恒定水平拉力F = 1240N，2s后小车受到的拉力发生了变化。试根据图象求：(g取10 m/s²）

（1）0 — 18时间内小车行驶的平均速度约为多少？
（2）t ="1" s时小车的加速度；
（3）小车与地面间的动摩擦因数。

如下图所示，在水平向右的匀强电场中，有一光滑绝缘导轨，导轨由水平部分和它连接的位于竖直平面的半圆环ABC构成，现距环最低点A为L的O处有一质量为m的带正电的小球，小球从静止开始沿水平轨道进入圆环，若小球所受电场力与其重力大小相等，圆环轨道的半径为R，则L必须满足什么条件才能使得小球在圆环上运动时不脱离圆环？

一根长为l的丝线吊着一质量为m，带电荷量为q的小球静止在水平向右的匀强电场中，如图所示，丝线与竖直方向成37°角，现突然将该电场方向变为向下且大小不变，不考虑因电场的改变而带来的其他影响(重力加速度为g)，求：

(1)匀强电场的电场强度的大小；(sin37°＝0.6，cos37°＝0.8)，
(2)小球经过最低点对丝线的拉力．

如图所示，半径为R的1/4光滑圆弧轨道与光滑水平面相切于B点，O为光滑圆弧的圆心，其中OB竖直，OC水平，且AB=R，整个空间存在水平向右的匀强电场，质量为m的带正电小球从A点静止释放，其所受电场力为重力的3/4倍，重力加速度为g，求：

（1）小球到达C点时对轨道的压力大小；
（2）小球从A点运动到C点过程中最大速度的大小．

如图所示，在竖直方向上A、B物体通过劲度系数为k的轻质弹簧相连，A放在水平地面上，B、C两物体通过细绳绕过光滑轻质定滑轮相连， C放在固定的光滑斜面上，斜面倾角为30°，用手按住物体C，使细绳刚刚拉直但无拉力作用，并保证ab段的细绳竖直、cd段的细绳与斜面平行。已知A、B的质量分别为m₁、m ₂，C的质量为2m，重力加速度为g，细绳与滑轮之间的摩擦力不计，开始时整个系统处于静止状态，释放物体C后它沿斜面下滑，斜面足够长，当C不再下滑时物体A恰不离开地面。求：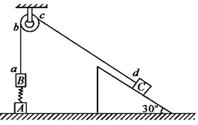

(1)物体A恰不离开地面时，物体C已下降的高度；
(2)其他条件不变，若把物体C换为质量为2（m+△m）的物体D ，释放物体D后它沿斜面下滑，当A刚要离开地面时，物体B的速度为多大？

(15分)在半径R=4000km的某星球表面，宇航员做了如下实验，实验装置如图甲所示，竖直平面内的光滑轨道由轨道AB和圆弧轨道BC组成，将质量m=0.2kg的小球从轨道上高H处的某点由静止滑下，用力传感器测出小球经过C点时对轨道的压力F，改变H的大小，可测出相应的F大小，F随H的变化关系如图乙所示，忽略星球自转。求：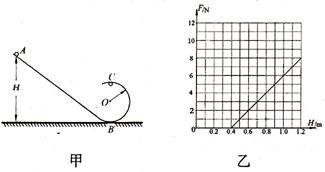

(1)圆弧轨道BC的半径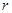；(2)该星球的第一宇宙速度。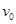