高中物理力学实验试题

北京奥运火炬成功登上珠峰，如图所示是火炬手攀登珠峰的线路图，据此图判断下列说法正确的是（    ）

A．由起点到终点火炬手所走线路的总长度等于位移

B．线路总长度与火炬手所用时间的比值等于火炬手的平均速度

C．在计算登山运动的速度时可以把火炬手当成质点

D．拉萨处的重力加速度要比北极的重力加速度小

如下图中，摆球A、B用细线悬挂在天花板上，两球刚好接触，现将摆球A在两摆线所在平面内向左拉开一小角度后释放，碰撞后，两摆球分开各自做简谐运动，以m_A、m_B分别表示A、B摆球的质量，则( )
　　A、如果m_A＞m_B，下一次碰撞将发生在平衡位置右侧
　　B、如果m_A＜m_B，下一次碰撞将发生在平衡位置左侧
　　C、无论两摆球的质量之比是多少，下一次碰撞都不可能在平衡位置右侧
　　D、无论两摆球的质量之比是多少，下一次碰撞都不可能在平衡位置左侧

把地球上的一个秒摆(周期等于2s的摆称为秒摆)拿到月球上去，它的振动周期变为多少？已知：地球质量M_地=5.98×10²⁴kg，半径R_地=6.4×10⁶m，月球质量M_月=7.34×10²²kg，半径R_月=1.74×10⁶m。

如图所示，若单摆处于沿水平方向作匀加速直线运动的系统内，单摆的摆长为L，系统水平向右的加速度为a，摆球的质量为m，求这一单摆的周期。

如图所示，将单摆小球A从静止释放的同时，高出悬点O的另一小球B做自由落体运动，结果它们同时到达跟单摆的平衡位置C等高处．已知摆长为l，偏角θ＜5°，求：B球的初位置与单摆悬点之间的高度差h．

如图所示，一个重为G的小球套在竖直放置的半径为R的光滑大圆球上，一个劲度系数为k，原长为L（L<R）的轻弹簧，一端固定在大圆环顶点A，另一端与小球相连小球在大圆环上无可摩擦滑动，求：当环静止于B点时，弹簧有多长？

下列关于速度和加速度的说法中，正确的是

A．物体运动的速度改变越大，它的加速度一定越大

B．物体运动的加速度等于零，它的速度不一定为零

C．物体运动的速度改变越小，它的加速度一定越小

D．物体运动的速度改变越快，它的加速度一定越大

下列关于速度和加速度的说法中，正确的是（  ）

A．物体速度的变化量越大，加速度越大

B．物体的速度变化越快，加速度越大

C．当加速度与速度方向相同且又减小时，物体却做加速运动

D．加速度为正值时，物体一定做加速运动

铁路提速要解决许多技术问题，其中提高机车牵引力功率是一个重要问题。已知列匀速运动时，列车所受附图与速度的平方成正比，即。设提速前速度为，速后速度为，则提速前与提速后，机车牵引力的功率之比为                        （   ）

A．

B．

C．

D．

一位质量m=50kg的滑雪运动员从高度h=30m的斜坡自由滑下（初速度为零）。斜坡的倾角θ=37°，滑雪板与雪面滑动摩擦因素=0.1。则运动员滑至坡底的过程中有：
（1）所受几个力所做的功各是多少？
（2）合力做了多少功？
（3）到达坡底时摩擦力的功率是多少？（不计空气阻力）

关于功率以下说法中正确的是：（　  ）     

A．据P＝W/t可知，机器做功越多，其功率就越大

B．据P＝Fv可知，汽车牵引力一定与速度成反比

C．据P＝W/t可知，只要知道在时间t内机器所做的功，就可求得这段时间内任一时刻机器做功的功率

D．根据P＝Fv可知，发动机功率一定时，汽车的牵引力与运动速度成反比

质量为、功率为P的汽车在平直公路上行驶，若汽车行驶时的功率恒为P，匀速运动的速度为，当汽车以速度（）行驶时，它的加速度是（阻力恒定）（   ）

A．P/mv2	B．P/m（v1－v2）
C．P（v1－v2）/mv1v2	D．P（v1＋v2）/ v1v2

下列关于力和运动关系的说法中，正确的是（           ）

A．没有外力作用时，物体不会运动，这是牛顿第一定律的体现

B．物体受力越大，运动得越快，这是符合牛顿第二定律的

C．物体所受合外力为0，则速度一定为0；物体所受合外力不为0，则其速度也一定不为0

D．物体所受的合外力最大时，速度却可以为0；物体所受的合外力为0时，速度却可以最大

一辆汽车从原点O由静止出发沿x轴做直线运动，为研究汽车运动的规律而记录下它在不同时刻的位置和速度，见下表所示．试求：

时刻t/s	0	1	2	3	4	5	6	7
位置坐标x/m	0	0.5	2	4.5	8	12	16	20
瞬时速度v/(m·s^－^1)	0	1	2	3	4	4	4	4

（1）汽车在3.5 s末的速度；
（2）前4 s内的平均加速度．

下列对加速度的定义式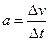的理解正确的是

A．加速度a与速度变化量Δv成正比

B．加速度a的大小由速度变化量Δv决定

C．加速度a的方向与Δv方向相同

D．加速度a的大小决定于速度变化率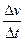