高中物理放射性同位素的应用计算题

平时擦玻璃时，我们经常会用到如图甲所示的“魔力刷”．使用时，两个一样的刷子分别位于玻璃窗户玻璃板的两侧，两刷子靠磁铁的吸引力吸在玻璃上，当移动其中一块刷子时，另一块刷子会跟到移动，达到同时清洁玻璃内外侧的目的．已知：某种品牌玻璃刷的每个刷子的质量都为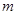，与玻璃的滑动摩擦因数均为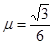，且最大静摩擦力等于滑动摩擦力，重力加速度取．

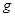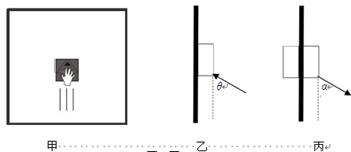
（1）将其中一个刷子用与竖直方向成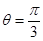的推力压在竖直玻璃上，如题9图乙所示，现要把刷子沿竖直方向向上推动，求推力的最小值
（2）把两个刷子对齐分别放在竖直玻璃板的两侧，如题9图丙所示，现用与竖直方向成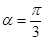，大小为的拉力向下拉动内侧的刷子时，外侧刷子将立即跟着移动且很快与内侧刷子保持相对静止．此时刷子磁铁间的吸引力在垂直玻璃板面方向的分量恒为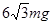，求刷子间的磁铁吸引力在沿玻璃板面切线方向的分量．
（3）假设玻璃是边长为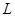的正方形，刷子是边长为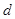的正方形；当两刷子的正对面积大于一半时，刷子磁铁间的吸引力的垂直分量和切向分量均不变，当两刷子的正对面积小于或等于一半时，两刷子就无法吸引在一起．在（2）的情况下，若拉力方向不变，大小变为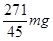，要使一次性向下拉动刷子就可以完成清理玻璃的竖边，求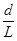的取值范围．

如图所示，一质量m＝1 kg的木板静止在光滑水平地面上．开始时，木板右端与墙相距L＝0.08 m，一质量m＝1 kg的小物块以初速度v₀＝2 m/s滑上木板左端．木板的长度可保证物块在运动过程中不与墙接触．物块与木板之间的动摩擦因数μ＝0.1，木板与墙碰撞后以与碰撞前瞬时等大的速度反弹．取g＝10 m/s²，求：

(1)从物块滑上木板到两者达到共同速度时，木板与墙碰撞的次数及所用的时间．
(2)达到共同速度时木板右端与墙之间的距离．

如图所示质量为m=1kg的滑块（可视为质点）由斜面上P点以初动能E_K0=20J沿斜面向上运动，当其向上经过Q点时动能E_KQ=8J，机械能的变化量ΔE_机=-3J，斜面与水平夹角α=37°。PA间距离l₀=0.625m，当滑块向下经过A点并通过光滑小圆弧后滑上质量M=0.25kg的木板 (经过小圆弧时无机械能损失），滑上木板瞬间触发一感应开关使木板与斜面底端解除锁定（当滑块滑过感应开关时，木板与斜面不再连接），木板长L=2.5m，木板与滑块间动摩擦因数µ₁=0.20，木板与地面的动摩擦因数µ₂=0.10。滑块带动木板在地面上向右运动，当木板与右侧等高光滑平台相碰时再次触发感应开关使木板与平台锁定。滑块沿平台向右滑上光滑的半径R=0.1m的光滑圆轨道（滑块在木板上滑行时，未从木板上滑下）。

求：①物块与斜面间摩擦力大小；
②木块经过A点时的速度大小v₁；
③为保证滑块通过圆轨道最高点，AB间距离d应满足什么条件？

如图所示，一个质量m=1kg的长木板静止在光滑的水平面上，并与半径为R=1.8m的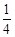光滑圆弧形固定轨道接触（但不粘连），木板的右端到竖直墙的距离为s=0.08m；另一质量也为m的小滑块从轨道的最高点由静止开始下滑，从圆弧的最低点A滑上木板。设长木板每次与竖直墙的碰撞时间极短且无机械能损失。木板的长度可保证物块在运动的过程中不与墙接触。已知滑块与长木板间的动摩擦因数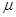=0.1，g取10m/s²。试求：

（1）滑块到达A点时对轨道的压力大小；
（2）当滑块与木板达到共同速度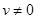（）时，滑块距离木板左端的长度是多少？

机场大道某路口，有按倒计时显示的时间显示灯。有一辆汽车在平直路面上以36Km/h 的速度朝该路口停车线匀速前进，在车头前端离停车线70 m 处司机看到前方绿灯刚好显示“5”。交通规则规定：绿灯结束时车头已越过停车线的汽车允许通过。
（1）若不考虑该路段的限速，司机的反应时间1s，司机想在剩余时间内使汽车做匀加速直线运动以通过停车线，则汽车的加速度a₁至少多大？
（2）若考虑该路段的限速，司机的反应时间为1s，司机反应过来后汽车先以a₂=2m/s²的加速度沿直线加速3 s，为了防止超速，司机在加速结束时立即踩刹车使汽车做匀减速直行，结果车头前端与停车线相齐时刚好停下来，求刹车后汽车加速度a₃大小（结果保留两位有效数字）

有一个竖直固定在地面的透气圆筒，筒中有一劲度系数为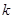的轻弹簧，其下端固定，上端连接一质量为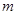的薄滑块，圆筒内壁涂有一层新型智能材料─—ER流体，它对滑块的阻力可调。起初，滑块静止，ER流体对其阻力为0，弹簧的长度为L.现有一质量也为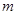的物体从距地面2L处自由落下，与滑块碰撞后粘在一起向下运动。为保证滑块做匀减速运动，且下移距离为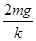时速度减为0，ER流体对滑块的阻力须随滑块下移而变。试求（忽略空气阻力）：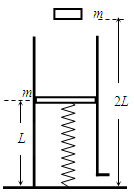

（1）下落物体与滑块碰撞前的瞬间物体的速度;
（2）下落物体与滑块碰撞过程中系统损失的机械能；
（3）滑块下移距离d时ER流体对滑块阻力的大小。

相距很近的平行板电容器，在两板中心各开有一个小孔，如图甲所示，靠近A板的小孔处有一电子枪，能够持续均匀地发射出电子，电子的初速度为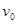，质量为m，电量为-e ，在AB 两板之间加上图乙所示的交变电压，其中0<k<1，；紧靠B 板的偏转电场电压也等于U₀，板长为L，两板间距为d，距偏转极板右端处垂直放置很大的荧光屏PQ。不计电子的重力和它们之间的相互作用，电子在电容器中的运动时间可以忽略不计。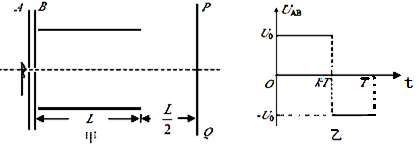

（1）试求在0—kT 与kT-T 时间内射出B 板电子的速度各多大？（结果用U₀、e、m表示）
（2）在0—T 时间内，荧光屏上有两个位置会发光，试求这两个发光点之间的距离。（结果用L、d 表示，）
（3）撤去偏转电场及荧光屏，当k 取恰当的数值时，使在0—T 时间内通过了电容器B 板的所有电子，能在某一时刻形成均匀分布的一段电子束，求k 值。

如图，在水平地面上有两物块甲和乙，它们的质量分别为2m、m，甲与地面间无摩擦，乙与地面间动摩擦因数为μ。现让甲物体以速度v₀向着静止的乙运动并发生正碰，试求：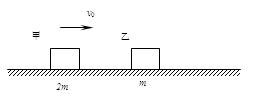

（i）甲与乙第一次碰撞过程中系统的最小动能；
（ii）若甲在乙刚停下来时恰好与乙发生第二次碰撞，则在第一次碰撞中系统损失了多少机械能？

减速带是交叉路口上常见的一种交通设施，在某小区门口有一橡胶减速带（如图），有一警用巡逻车正以最大速度20m/s从小区门口经过，在离减速带50m时警察发现一逃犯正以10m/s的速度骑电动车匀速通过减速带，而巡逻车要匀减速到5m/s通过减速带（减速带的宽度忽略不计），减速到5m/s后立即以2.5m/s²的加速度继续追赶，设在整个过程中，巡逻车与逃犯均在水平直道上运动，求从警察发现逃犯到追上逃犯需要的时间。

如图所示，一个物块A（可看成质点）放在足够长的平板小车B的右端，A、B一起以v₀的水平初速度沿光滑水平面向左滑行．左边有一固定的竖直墙壁，小车B与墙壁相碰，碰撞时间极短，且碰撞前、后无动能损失．已知物块A与小车B的水平上表面间的动摩擦因数为μ，重力加速度为g．

（1）若A、B的质量均为m，求小车与墙壁碰撞后的运动过程中，物块A所受摩擦力的冲量大小和方向；
（2）若A、B的质量比为k,且k＜1，求物块A在小车B上发生相对运动的过程中物块A对地的位移大小；
（3）若A、B的质量比为k，且k=2，求小车第一次与墙壁碰撞后的运动过程所经历的总时间．

如图所示（1），在粗糙的水平地面上，放有一块质量为m="1" kg，初速度为v₀的木块，现在加水平恒力F，方向与初速度的方向在同一条直线上，通过实验发现不同的F，物块在地面运动的时间t不同，且当－2 N≤F＜2 N时，1/t与F的关系如图（2）所示（设v₀的方向为正、滑动摩擦力等于最大静摩擦力），则

（1）物块的初速度为多少？
（2）物块与地面间的动摩擦因素为多少？
（3）物块运动的时间t可能等于0.4 s吗？说明原因．

如图所示水平传送带，轮的半径均为 1/π，顺时针转动，两轮轴心相距L=8.0m。将一物体轻放在传送带左端，物体与传送带间的动摩擦因数为μ=0.4。

（1）当传送带以v₀=4.0m/s的速度匀速运动时,物体由A端运送到B端所用时间为多少?
（2）要想尽快将物体由A端送到B端（设初速度仍为零），轮的转速至少应为多大?
（3）在运送物体的过程中物体会在传送带上留下划痕。当物体静止释放在A端时，传送带做初速度v₀ =    m/s的匀减速运动，物体刚好到达B端，求传送带的加速度大小和划痕的长度 。（结果可用分数表示）

(12分)在一段平直的公路上,质量为2×10³ kg的汽车从静止开始做匀加速运动,经过2 s,速度达到10 m/s。随后汽车以P=6×10⁴ W的额定功率沿平直公路继续前进,又经过50 s达到最大速度。设汽车所受的阻力恒定,大小为1.5×10³ N。求:
(1)汽车行驶的最大速度的大小。
(2)汽车的速度为20 m/s时的加速度大小。
(3)汽车从静止到达到最大速度所经过的路程。

如图所示，在光滑绝缘的水平面上，放置两块直径为2L的同心半圆形金属板A、B，两板间的距离很近，半圆形金属板A、B的左边有水平向右的匀强电场E₁，半圆形金属板A、B之间存在电场，两板间的电场强度E₂可认为大小处处相等，方向都指向O，现从正对A、B板间隙、到两板的一端距离为d处静止释放一个质量为m、电荷量为q的带正电微粒（不计重力），此微粒恰能在两板间运动且不与板发生相互作用．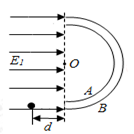

（1）求半圆形金属板A、B之间电场强度的E₂的大小？
（2）从释放微粒开始，经过多长时间微粒的水平位移最大？

如图所示，电阻不计、间距L=1m、足够长的光滑金属导轨ab、cd与水平面成θ=37°角，导轨平面矩形区域efhg内分布着磁感应强度的大小B=1T，方向垂直导轨平面向上的匀强磁场，边界ef、gh之间的距离D=1.4m。现将质量m=0.1kg、电阻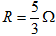的导体棒P、Q相隔Δt=0.2s先后从导轨顶端由静止自由释放，P、Q在导轨上运动时始终与导轨垂直且接触良好，P进入磁场时恰好匀速运动，Q穿出磁场时速度为2.8m/s。已知重力加速度g=10m/s²，sin37°=0.6，求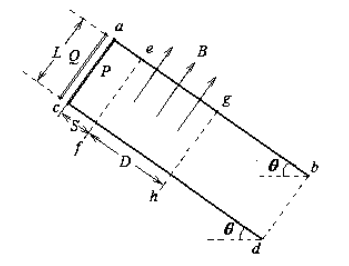

（1）导轨顶端与磁场上边界ef之间的距离S；
（2）从导体棒P释放到Q穿出磁场的过程，回路中产生的焦耳热Q_总。