如图所示，光滑平行的水平金属导轨MN、PQ相距d,在M点和P点间接一个阻值为R的电阻，在两导轨间OO1O1′O′矩形区域内有垂直导轨平面竖直向下、宽为l的匀强磁场，磁感应强度大小为B；质量为m，电阻为r的导体棒ab，垂直搁在导轨上，与磁场左边界相距l0，现用一大小为F、水平向右的恒力拉ab棒，使它由静止开始运动，棒ab在离开磁场前已经做匀速直线运动（棒ab与导轨始终保持良好的接触，导轨电阻不计）．求：
⑴棒ab在离开磁场右边界时的速度；
⑵棒ab通过磁场区域的过程中通过电阻R的电荷量．
如图所示，在倾角θ＝30°的斜面上，固定一金属框，宽l＝0.25 m，接入电动势E＝12 V、内阻不计的电池．垂直框面放置一根质量m＝0.2 kg的金属棒ab，它与框架间的动摩擦因数μ＝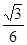
，整个装置放在磁感应强度B＝0.8 T、垂直框面向上的匀强磁场中。当调节滑动变阻器R的阻值在什么范围内时，可使金属棒静止在框架上？(框架与金属棒的电阻不计，g取10 m/s2)
如图所示，在同一水平面的两导轨相互平行，并处在竖直向上的匀强磁场中，磁感应强度B=2T，一根质量为m=2kg的金属棒垂直导轨方向放置。导轨间距为0.5m，已知金属棒与导轨间的摩擦因数μ="0.05" ，当金属棒中的电流为5A时，金属棒做匀加速直线运动；求金属棒加速度的大小。
如图所示，两根足够长的光滑金属导轨，相距为L=10cm，竖直放置，导轨上端连接着电阻R1=1Ω，质量为m=0.01kg、电阻为R2=0.2Ω的金属杆ab与导轨垂直并接触良好，导轨电阻不计。整个装置处于与导轨平面垂直的磁感应强度为B=1T的匀强磁场中。ab杆由静止释放，经过一段时间后达到最大速率，g取10m/s2，求此时：
⑴杆的最大速率；
⑵ab间的电压；
⑶电阻R1消耗的电功率。
如图所示，在匀强磁场中有一倾斜的平行金属导轨，导轨间距为L=0.2m，长为2d，d=0.5m，上半段d导轨光滑，下半段d导轨的动摩擦因素为μ=
，导轨平面与水平面的夹角为θ=30°．匀强磁场的磁感应强度大小为B=5T，方向与导轨平面垂直．质量为m=0.2kg的导体棒从导轨的顶端由静止释放，在粗糙的下半段一直做匀速运动，导体棒始终与导轨垂直，接在两导轨间的电阻为R=3Ω，导体棒的电阻为r=1Ω，其他部分的电阻均不计，重力加速度取g=10m/s2，求：
（1）导体棒到达轨道底端时的速度大小；
（2）导体棒进入粗糙轨道前，通过电阻R上的电量q；
（3）整个运动过程中，电阻R产生的焦耳热Q．
如图所示，U形导轨固定在水平面上，右端放有质量为m的金属棒ab，ab与导轨间的动摩擦因数为μ，金属棒与导轨围成正方形，边长为L，金属棒接入电路的电阻为R，导轨的电阻不计．从t=0时刻起，加一竖直向上的匀强磁场，其磁感应强度随时间的变化规律为B=kt，（k>0），设金属棒与导轨间的最大静摩擦力等于滑动摩擦力．
（1）求金属棒滑动前，通过金属棒的电流的大小和方向；
（2）t为多大时，金属棒开始移动？
（3）从t=0时刻起到金属棒开始运动的过程中，金属棒中产生的焦耳热多大？
如图所示，在倾角为θ＝30°的斜面上，固定一宽L＝0.25 m的平行金属导轨，在导轨上端接入电源和滑动变阻器R.电源电动势E＝12 V，内阻r＝1 Ω，一质量m＝20 g的金属棒ab与两导轨垂直并接触良好．整个装置处于磁感应强度B＝0.80 T、垂直于斜面向上的匀强磁场中(导轨与金属棒的电阻不计)．金属导轨是光滑的，取g＝10 m/s2，要保持金属棒在导轨上静止，求：
(1)金属棒所受到的安培力的大小．
(2)通过金属棒的电流的大小．
(3)滑动变阻器R接入电路中的阻值．
(18分)如图所示，两条平行的光滑金属导轨固定在倾角为θ的绝缘斜面上，导轨上端连接一个定值电阻。导体棒a和b放在导轨上，与导轨垂直并良好接触。斜面上水平虚线PQ以下区域内，存在着垂直穿过斜面向上的匀强磁场。现对a棒施以平行导轨斜向上的拉力，使它沿导轨匀速向上运动，此时放在导轨下端的b棒恰好静止。当a棒运动到磁场的上边界PQ处时，撤去拉力， a棒将继续沿导轨向上运动一小段距离后再向下滑动，此时b棒已滑离导轨。当a棒再次滑回到磁场上边界PQ处时，又恰能沿导轨匀速向下运动。已知a棒、b棒和定值电阻的阻值均为R，b棒的质量为m，重力加速度为g， 导轨电阻不计。求
（1）a棒在磁场中沿导轨向上运动的过程中，a棒中的电流大小Ia与定值电阻R中的电流大小IR之比；
（2）a棒质量ma；
（3）a棒在磁场中沿导轨向上运动时所受的拉力F。
如图所示，PQ和MN是固定于水平面内的平行光滑金属轨道，轨道足够长，其电阻可忽略不计。金属棒ab、cd放在轨道上，始终与轨道垂直，且接触良好。金属棒ab、cd的质量均为m，长度均为L。两金属棒的长度恰好等于轨道的间距，它们与轨道形成闭合回路。金属棒ab的电阻为2R，金属棒cd的电阻为R。整个装置处在竖直向上、磁感应强度为B的匀强磁场中。
（1）若保持金属棒ab不动，使金属棒cd在与其垂直的水平恒力F作用下，沿轨道以速度v做匀速运动。试推导论证：在Δt时间内，F对金属棒cd所做的功W等于电路获得的电能E电；
（2）若先保持金属棒ab不动，使金属棒cd在与其垂直的水平力F′（大小未知）作用下，由静止开始向右以加速度a做匀加速直线运动，水平力F′作用t0时间撤去此力，同时释放金属棒ab。求两金属棒在撤去F′后的运动过程中，
①金属棒ab中产生的热量；
②它们之间的距离改变量的最大值Dx。
如图所示，两根足够长的直金属导轨MN、PQ平行放置在倾角为θ的绝缘斜面上，两导轨间距为L。一根质量为m的均匀直金属杆ab放在两导轨上，并与导轨垂直，且接触良好，整套装置处于匀强磁场中。金属杆ab中通有大小为I的电流。已知重力加速度为g。
（1）若匀强磁场方向垂直斜面向下，且不计金属杆ab和导轨之间的摩擦，金属杆ab静止在轨道上，求磁感应强度的大小；
（2）若金属杆ab静止在轨道上面，且对轨道的压力恰好为零。试说明磁感应强度大小和方向应满足什么条件；
（3）若匀强磁场方向垂直斜面向下，金属杆ab与导轨之间的动摩擦因数为μ，且最大静摩擦力等于滑动摩擦力。欲使金属杆ab静止，则磁感应强度的最大值是多大。
如图所示，竖直向上的匀强磁场，零时刻磁感应强度B0为2T，之后以1T/s在变大，水平轨道电阻不计，且不计摩擦阻力。宽L=2m的导轨上放一电阻r=lΩ的导体棒，并用水平线通过定滑轮吊着质量M=2kg（g=10m/s2）的重物，轨道左端连接的电阻R=19Ω，图中的l=1m，求：
（1）重物被吊起前感生电流大小；
（2）零时刻起至少经过多长时间才能吊起重物．
如图所示，PQ和MN为水平、平行放置的金属导轨，相距1m，导体棒ab跨放在导轨上，棒的质量m=0.2kg，棒的中点用细绳经滑轮与物体相连，物体质量M=0.3kg，棒与导轨间的动摩擦因数
=0.5，匀强磁场的磁感应强度B=2T，方向竖直向下，为了使物体保持静止，应在棒中通入多大的电流？方向如何？
如图所示，在倾角为θ＝30°的斜面上，固定一宽L＝0.25 m的平行金属导轨，在导轨上端接入电源和滑动变阻器R.电源电动势E＝12 V，内阻r＝1Ω，一质量m＝20g的金属棒ab与两导轨垂直并接触良好．整个装置处于磁感应强度B＝0.80 T、垂直于斜面向上的匀强磁场中(导轨与金属棒的电阻不计)．金属导轨是光滑的，取g＝10 m/s2，要保持金属棒在导轨上静止，求：
(1)金属棒所受到的安培力大小；
(2)通过金属棒的电流；
(3)滑动变阻器R接入电路中的阻值．
如图所示，PQ和MN为水平、平行放置的金属导轨，相距1m，导体棒ab跨放在导轨上，棒的质量m=0.2㎏，棒的中点用细绳经滑轮与物体相连，物体质量M=0.3㎏，棒与导轨间的动摩擦因数
=0.5，匀强磁场的磁感应强度B=2T，方向竖直向下，为了使物体保持静止，应在棒中通入多大的电流？方向如何？
(12分)如图所示，两足够长的平行光滑的金属导轨MN、PQ相距为L，导轨平面与水平面的夹角
=30°，导轨电阻不计，磁感应强度为B的匀强磁场垂直于导轨平面向上。长为L的金属棒
垂直于MN、PQ放置在导轨上，且始终与导轨接触良好，金属棒的质量为
、电阻为R。两金属导轨的上端连接一个灯泡，灯泡的电阻也为R。现闭合开关K ，给金属棒施加一个方向垂直于杆且平行于导轨平面向上的、大小为F＝2mg的恒力，使金属棒由静止开始运动，当金属棒达到最大速度时，灯泡恰能达到它的额定功率。重力加速度为g，求：
（1）金属棒能达到的最大速度vm；
（2）灯泡的额定功率PL；
（3）若金属棒上滑距离为s时速度恰达到最大，求金属棒由静止开始上滑2s的过程中，金属棒上产生的电热Q1。
粤公网安备 44130202000953号