高中物理电势计算题

在科学研究中，可以通过施加适当的电场和磁场来实现对带电粒子运动的控制。如图所示，某时刻在xOy平面内的第Ⅱ、Ⅲ象限中施加沿y轴负方向、电场强度为E的匀强电场，在第Ⅰ、Ⅳ象限中施加垂直于xOy坐标平面向里、磁感应强度为B的匀强磁场。一质量为m，电荷量为q的带正电的粒子从M点以速度v₀沿垂直于y轴方向射入该匀强电场中，粒子仅在电场力作用下运动到坐标原点O且沿OP方向进入第Ⅳ象限。在粒子到达坐标原点O时撤去匀强电场（不计撤去电场对磁场及带电粒子运动的影响），粒子经过原点O进入匀强磁场中，并仅在磁场力作用下，运动一段时间从y轴上的N点射出磁场。已知OP与x轴正方向夹角α=60°，带电粒子所受重力及空气阻力均可忽略不计，求：

（1）M、O两点间的电势差U；
（2）坐标原点O与N点之间的距离d；
（3）粒子从M点运动到N点的总时间t。

如图所示，在匀强电场中，有A、B两点，它们间距为2cm，两点的连线与场强方向成60°角。将一个电量为−2×10⁻⁵C的电荷由A移到B，其电势能增加了0．1J 。则：

（1）在此过程中，电场力对该电荷做了多少功？
（2）A、B两点的电势差U_AB为多少？
（3）匀强电场的场强为多大？

如图，质量为m、电量为 e的电子，从A点以速度v₀垂直场强方向射入匀强电场中，从B点射出电场时的速度方向与电场线成120^o角，问A、B两点间的电势差是多少？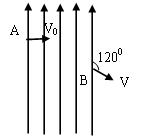

在匀强电场中，将一电荷量为2×10^-5C的负电荷由M点移到N点，其电势能增加了10^-3Ｊ，已知M、N间的距离为2cm，两点连线与电场线（方向未知）成60⁰角，如图所示。

（1）在图上标出电场线的方向
（2）M、N两点间的电势差U_MN等于多少？ 设M点电势为0，则N点电势φ_N等于多少？
（3）该匀强电场的场强为多大？

如果把带电量为C的点电荷从无穷远移至电场中的 A点，需克服电场力做功J。试求：
（1）q在A点的电势能和在A点的电势（取无穷远处电势为零）。
（2）q未移入电场前A点的电势是多少？

有一带电荷量q＝－3×10^－6 C的点电荷，从电场中的A点移到B点时，克服静电力做功6×10^－4 J，从B点移到C点，静电力做功9×10^－4 J．问：
(1)AB、BC间电势差各为多少？
(2)如以B点电势为零，则A、C两点的电势各为多少？电荷在A、C两点的电势能各为多少？

如图，将电荷量为的点电荷从匀强电场中的A点移动到B点，AB=2cm，电场力做的功为，

（1）A、B两点的电势差；（2）求匀强电场的场强E

真空中存在空间范围足够大的，水平向右的匀强电场。在电场中，若将一个质量为m、带正电的小球由静止释放，运动中小球的速度与竖直方向夹角为37°（取sin37°= 0.6， cos37°= 0.8）。现将该小球从电场中某点以初速度v₀竖直向上抛出。求运动过程中
（1）小球受到的电场力的大小及方向；
（2）小球从抛出点至最高点的电势能变化量；

普朗克常量h＝6.63×10^－34 J·s，铝的逸出功W₀＝6.72×10^－19 J，现用波长λ＝200 nm的光照射铝的表面(结果保留三位有效数字)．
①求光电子的最大初动能；
②若射出的一个具有最大初动能的光电子正对一个距离足够远且静止的电子运动，求在此运动过程中两电子电势能增加的最大值(除两电子间的相互作用以外的力均不计)。

在电场中把电量为2.0×10^-9C的正电荷从A点移到B点，电场力做功1.5×10^-7J，再把这个电荷从B点移到C点，克服电场力做功4.0×10^-7J．
(1)求A、C两点间电势差
(2)电荷从A经B移到C，电势能的变化怎样

如图所示，光滑水平细杆MN、CD，MN、CD在同一竖直平面内。两杆间距离为h，N、C连线左侧存在有界的电场，电场强度为E。质量为m的带正电的小球P，穿在细杆上，从M端点由静止向N端点运动，在N、C连线中点固定一个带负电的小球，电荷量为Q。在匀强电场中做匀速圆周运动恰好回到C点，且小球P与细杆之间相互绝缘。

求：①带正电的小球P的电荷量q ，
②小球P在细杆MN上滑行的末速度v₀；
③光滑水平细杆M、N两点之间的电势差；

如图A、B、C、D为一匀强电场中的四个点，它们正好是一个矩形的四个顶点，其中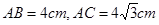，电场线与矩形所在平面平行。已知将的正电荷从A点移到B点，电场力做功；将这个电荷从B移到C点电势能增加了，设A点电势为零。求：

（1）B点和C点的电势
（2）匀强电场的电场强度大小和方向

如图所示，一根长为l＝1.5 m的绝缘细直杆MN，竖直固定在场强为E＝1.0×10⁵ N／C、与水平方向成θ＝37°角的倾斜向上的匀强电场中。杆的下端M固定一个带电小球A，电荷量Q＝＋4.5×10^－6 C；另一带电小球B穿在杆上可自由滑动，电荷量q＝＋1.0×10^－6 C，质量m＝1.0×10^－2 kg，与杆之间的动摩擦因数μ＝0.1。现将小球B从杆的上端N静止释放，小球B开始运动。（静电力常量k＝9.0×10⁹ N·m²／C²。取g＝10 m／s²；sin37º＝0.6，cos37º＝0.8）

（1）小球B开始运动时的加速度为多大；
（2）小球B的速度最大时，距M端的高度h为多大；
（3）若小球B在下落过程中的最大速度为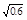m／s，则从开始下落到速度达到最大的过程中，小球B的电势能改变了多少。

空间有一匀强电场，电场方向与纸面平行。一带正电，电量为q，质量为m的小球（重力不计），在恒定拉力F的作用下沿虚线以速度由M匀速运动到N，如图所示．已知力F和MN间夹角为，MN间距离为L，则：

（1）匀强电场的电场强度大小为多少？
（2）MN两点的电势差为多少？
（3）当带电小球到达N点时，撤去外力F，则小球回到过M点的等势面时的动能为多少？

把一检验电荷q放在点电荷Q所形成的电场中的A点，若检验电荷的电量为q=－2.0×10^－8C，它所受的电场力F=2.0×10^—3N，方向背向Q，如图所示，

求：（1）A点的场强大小。
（2）若将检验电荷q从电场中的A点移到B点，电场力做功为4.0×10^－6 J，则A、B之间的电势差是多少？