高中物理电荷守恒定律试题

如图所示，光滑半圆弧轨道半径为r，OA为水平半径，BC为竖直直径。一质量为m 的小物块自A处以某一竖直向下的初速度滑下，进入与C点相切的粗糙水平滑道CM上。在水平滑道上有一轻弹簧，其一端固定在竖直墙上，另一端恰位于滑道的末端C点（此时弹簧处于自然状态）。若物块运动过程中弹簧最大弹性势能为E_p，且物块被弹簧反弹后恰能通过B点。已知物块与水平滑道间的动摩擦因数为μ，重力加速度为g，求：

（1）物块被弹簧反弹后恰能通过B点时的速度大小；
（2）物块离开弹簧刚进入半圆轨道c点时受轨道支持力大小；
（3）物块从A处开始下滑时的初速度大小v₀。

如图所示，一辆质量为M＝2kg的平板小车A停靠在竖直光滑墙处，地面水平且光滑，一质量为m＝1kg的小铁块B（可视为质点）放在平板小车A最右端，平板小车A上表面水平且与小铁块B之间的动摩擦因数μ＝0.5。现给小铁块B一个v₀＝5m/s的初速度使之向左运动，与竖直墙壁发生弹性碰撞（无动能损失）后向右运动，求小车的车长多长时，才会使小物块恰好回到小车的最右端。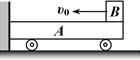

如图所示，在水平方向的匀强电场中有一表面光滑、与水平面成45°角的绝缘直杆AC，其下端(C端)距地面高度h＝0.8 m．有一质量为500 g的带电小环套在直杆上，正以某一速度沿杆匀速下滑．小球离杆后正好通过C端的正下方P点处．(g取10 m/s²)求：
 
(1)小环离开直杆后运动的加速度大小和方向；
(2)小环从C运动到P过程中的动能增量；
(3)小环在直杆上匀速运动时速度的大小v₀.

(10分)一子弹击中木板时的速度是800 m/s，历时0.2 s穿出木板，穿出时子弹的速度为300 m/s，则子弹穿过木板时的加速度为多少？

如图所示，一轻质弹簧上端悬挂于天花板，下端系一质量为2m的金属板A处于平衡状态。在距物体A正上方高为h处有一个质量为m的圆环B由静止下落，与弹簧下端的金属板A碰撞(碰撞时间极短)而后两者以相同的速度运动。不计空气阻力，两物体均可视为质点。重力加速度为g。求：
 
①碰撞结束瞬间两物体的速度大小；
②碰撞结束后两物体以相同的速度一起向下运动，当两者第一次到达最低点时，两者相互作用力的冲量大小为I，该过程这两者相互作用平均作用力为多大？

如图所示，在倾角θ=30°、足够长的斜面上分别固定着相距L=0.2m的A、B两个物体，它们的质量为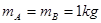，与斜面间动摩擦因数分别为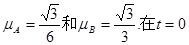时刻同时撤去固定两物体的外力后，A物体沿斜面向下运动，并与B物体发生连续碰撞（碰撞时间极短忽略不计），每次碰后两物体交换速度（g=10m/s²）求：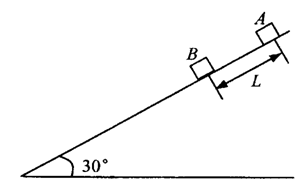

（1）A与B第一次碰后瞬时B的速率？
（2）从A开始运动到两物体第二次相碰经历多长时间？
（3）至第n次碰撞时A、B两物块通过的路程分别是多少？

如图所示，质量为M的木板，静止放置在粗糙水平地面上，有一个可视为质点的小物块质量为m，以某一水平初速度从左端冲上木板．从物块冲上木板到物块和木板达到共同速度的过程中，物块和木板的 t图象分别如图中的折线acd和bcd所示，a、b、c、d点的坐标为a(0，10)、b(0，0)、c(4，4)、d(12，0)．根据 t图象，求：
 
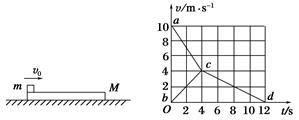
(1) 物块相对木板滑行的距离Δx；
(2) 物块质量m与木板质量M之比。

矩形滑块由不同材料的上、下两层粘合在一起组成，将其放在光滑的水平面上，质量为m的子弹以速度v水平射向滑块。若射击下层，子弹刚好不射出；若射击上层，则子弹刚好能射穿一半厚度，如图所示。则上述两种情况相比较（  ）

A．子弹的末速度大小相等

B．系统产生的热量一样多

C．子弹对滑块做的功不相同

D．子弹和滑块间的水平作用力一样大

如图所示，在粗糙水平台阶上放置一质量m=0.5kg的小物块，它与水平台阶间的动摩擦因数μ=0.5，与台阶边缘O点的距离s=5m。在台阶右侧固定一个圆弧挡板，圆弧半径R=1m，圆弧的圆心也在O点。今以O点为原点建立平面直角坐标系xOy。现用F=5N的水平恒力拉动小物块，一段时间后撤去拉力，小物块最终水平抛出并击中挡板。（，取g=10m/s²）

（1）若小物块恰能击中挡板上的P点（OP与水平方向夹角为37°），求其离开O点时的速度大小；
（2）为使小物块击中挡板，求拉力F作用的最短时间；
（3）改变拉力F的作用时间，使小物块击中挡板的不同位置，求击中挡板时小物块动能的最小值。

如图所示，在光滑的水平面上有A、B两小车，质量均为M=30kg，A车上有一质量为m=60kg的人。A车以大小为υ=2m/s的速度正对着静止的B车冲去，A车上的人至少要以多大的水平速度（相对地）从A车跳到B车上，才能避免两车相撞？

(17分)如图,在光滑的水平长轨道上,质量为m的小球P₁和质量M的小球P₂分别置于A、C两点,从某时刻起,P₁始终受到向右的大小恒定为F的力作用而向右运动,到C点时与P₂发生水平对心正碰（碰撞时间很短,可忽略不计）,碰后瞬间P₁速度变为零.已知AC、BC间距离分别为L_AC=2L，L_CB=L，M=3m.试求：

(1)碰后瞬间P₂的速度大小;
（2）两球第二次碰撞前的最大距离d_m .

(13分)如图所示，在沙堆表面放置一长方形木块A，其上面再放一个质量为m=0.10kg的爆竹B，木块的质量为M=6.0kg。当爆竹爆炸时，因反冲作用使木块陷入沙中深度h=5cm，而木块所受的平均阻力为f=80N。若爆竹的火药质量以及空气阻力可忽略不计，g取10m/s²，求爆竹能上升的最大高度。

如图所示，质量为km的斜劈，其中k>1，静止放在光滑的水平面上，斜劈的曲面光滑且为半径为R的四分之一圆面，圆面下端与光滑水平面相切。一质量为m的小球位于水平面上某位置，现给小球水平向右的初速度v₀。

①若R足够大，求当小球从斜劈滑下离开时小球的速度；
②若小球向右滑上斜劈刚好没有越过圆面上端，求k的取值 .

用质子流()轰击固态的重水，当质子和重水中的氘核()发生碰撞时，系统损失的动能如果达到核反应所需的能量，将发生生成核的反应。
①写出质子流轰击固态的重水的核反应方程；
②当质子具有最小动能时，用质子流轰击固态的重水（认为氘核是静止的）可发生核反应；若用氘核轰击普通水的固态冰中的质子（认为质子是静止的）时，也能发生同样的核反应，求氘核的最小动能。已知氘核质量等于质子质量的两倍。

光滑水平面上有三个物块A、B和C位于同一直线上，如图所示，B的质量为m=1kg，A、C的质量都是3m，开始时三个物块都静止，让B获得向右的初速度v₀=2m/s，先与C发生弹性碰撞，然后B又与A发生碰撞并黏在一起，求B在前、后两次碰撞中受到的冲量大小之比．