用质子流(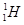 )轰击固态的重水
)轰击固态的重水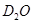 ,当质子和重水中的氘核(
,当质子和重水中的氘核(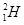 )发生碰撞时,系统损失的动能如果达到核反应所需的能量,将发生生成
)发生碰撞时,系统损失的动能如果达到核反应所需的能量,将发生生成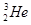 核的反应。
核的反应。
①写出质子流轰击固态的重水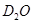 的核反应方程;
的核反应方程;
②当质子具有最小动能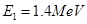 时,用质子流轰击固态的重水
时,用质子流轰击固态的重水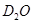 (认为氘核是静止的)可发生核反应;若用氘核轰击普通水的固态冰中的质子(认为质子是静止的)时,也能发生同样的核反应,求氘核的最小动能
(认为氘核是静止的)可发生核反应;若用氘核轰击普通水的固态冰中的质子(认为质子是静止的)时,也能发生同样的核反应,求氘核的最小动能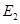 。已知氘核质量等于质子质量的两倍。
。已知氘核质量等于质子质量的两倍。
用质子流(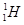 )轰击固态的重水
)轰击固态的重水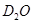 ,当质子和重水中的氘核(
,当质子和重水中的氘核(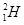 )发生碰撞时,系统损失的动能如果达到核反应所需的能量,将发生生成
)发生碰撞时,系统损失的动能如果达到核反应所需的能量,将发生生成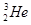 核的反应。
核的反应。
①写出质子流轰击固态的重水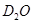 的核反应方程;
的核反应方程;
②当质子具有最小动能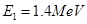 时,用质子流轰击固态的重水
时,用质子流轰击固态的重水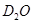 (认为氘核是静止的)可发生核反应;若用氘核轰击普通水的固态冰中的质子(认为质子是静止的)时,也能发生同样的核反应,求氘核的最小动能
(认为氘核是静止的)可发生核反应;若用氘核轰击普通水的固态冰中的质子(认为质子是静止的)时,也能发生同样的核反应,求氘核的最小动能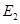 。已知氘核质量等于质子质量的两倍。
。已知氘核质量等于质子质量的两倍。