高中物理人造卫星计算题

质量为m的登月器与航天飞机连接在一起，随航天飞机绕月球做半径为3R（ R为月球半径）的圆周运动。当它们运行到轨道的A点时，登月器被弹离, 航天飞机速度变大，登月器速度变小且仍沿原方向运动，随后登月器沿椭圆登上月球表面的B点，在月球表面逗留一段时间后，经快速起动仍沿原椭圆轨道回到分离点A与航天飞机实现对接。已知月球表面的重力加速度为g_月。科学研究表明，天体在椭圆轨道
上运行的周期的平方与轨道半长轴的立方成正比。试求：
（1）登月器与航天飞机一起在圆周轨道上绕月球运行的周期是多少？
（2）若登月器被弹射后,航天飞机的椭圆轨道长轴为8R，则为保证登月器能顺利返回A点，登月器可以在月球表面逗留的时间是多少？

目前，我国探月工程已取得重大进展。在不久的将来，我国宇航员将登上月球。假如给你提供三组信息：①一同学在家中用长为L的细线和一个小螺丝帽组成了一个单摆，测得该单摆的振动周期为T；②一宇航员在月球表面上以初速度v₀竖直上抛一小球，经过时间t，小球落回原处；③地球的质量约为月球质量的81倍，地球半径为R。 
请你根据以上信息求：
（1）地球表面的重力加速度。
（2）月球表面的重力加速度。
（3）月球的半径。

在勇气号火星探测器着陆的最后阶段，着陆器降落到火星表面上，再经过多次弹跳才停下来。假设着陆器第一次落到火星表面弹起后，到达最高点时高度为h，速度方向是水平的，速度大小为v₀，求它第二次落到火星表面时速度的大小，计算时不计火星大气阻力。已知火星的一个卫星的圆轨道的半径为r，周期为T。火星可视为半径为r₀的均匀球体。

2005年10月17日，我国第二艘载人飞船“神州六号”，在经过了115个小时32分钟的太空飞行后顺利返回。
　　（1）飞船在竖直发射升空的加速过程中，宇航员处于超重状态。设点火后不久，仪器显示宇航员对座舱的压力等于他体重的4倍，求此时飞船的加速度大小。地面附近重力加速度g = 10m/s²。
　　（2）飞船变轨后沿圆形轨道环绕地球运行，运行周期为T。已知地球半径为R，地球表面的重力加速度为g。求飞船离地面的高度。

搭载有“勇气”号火星车的探测器成功登陆在火星表面 。“勇气”号离火星地面12m时与降落伞自动脱离，被众气囊包裹的“勇气”号下落到地面后又弹跳到15m高处，这样上下碰撞了若干次后，才静止在火星表面上。假设“勇气”号下落及反弹运动均沿竖直方向。已知火星的半径为地球半径的二分之一，质量为地球的九分之一（取地球表面的重力加速度为10m/s²）。 
（1）根据上述数据，火星表面的重力加速度是多少？
（2）若被众气囊包裹的“勇气”号第一次碰火星地面时，其机械能损失为其12m高处与降落伞脱离时的机械能的20﹪，不计空气的阻力，求“勇气”号与降落伞脱离时的速度。

“神州七号”飞船的成功飞行为我国在2010年实现探月计划——“嫦娥工程”获得了宝贵的经验．假设月球半径为R，月球表面的重力加速度为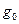，飞船在距月球表面高度为3R的圆形轨道Ⅰ运动，到达轨道的A点点火变轨进入椭圆轨道Ⅱ，到达轨道的近月点B再次点火进入月球近月轨道Ⅲ绕月球作圆周运动．求：
（1）飞船在轨道Ⅰ上的运行速率；
（2）飞船在轨道Ⅲ绕月球运行一周所需的时间．

航天宇航员在月球表面完成了如下实验：如图所示，在月球表面固定一竖直光滑圆形轨道，在轨道内的最低点，放一可视为质点的小球，当给小球水平初速度v₀时，小球刚好能在竖直面内做完整的圆周运动。已知引力常量为G，圆形轨道半径为r，月球的半径为R。求: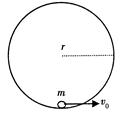

（1）月球表面的重力加速度g；
（2）月球的质量M；
（3）若在月球表面上发射一颗环月卫星，其最小发射速度。

发射地球同步卫星时，先将卫星发射到距地面高度为h₁的近地圆轨道上，在卫星经过A点时点火实施变轨进入椭圆轨道，最后在椭圆轨道的远地点B点再次点火将卫星送入同步轨道，如图所示。已知同步卫星的运动周期为T，地球的半径为R，地球表面重力加速度为g，求：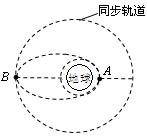

（1）卫星在近地点A的加速度大小；
（2）远地点B距地面的高度。

2007年10月24日我国成功发射了“嫦娥一号”绕月卫星，我国计划2020年实现载人登月，若你通过努力学习、刻苦训练有幸成为中国登月第一人，而你为了测定月球表面附近的重力加速度进行了如下实验：
在月球表面上空让一个小球由静止开始自由下落，测出下落高度h=20m时，下落的时间正好为t=5s，则：
（1）月球表面的重力加速度g_月为多大？
（2）小球下落2．5s时的瞬时速度为多大？

继1999年11月20日我国“神州一号”无人驾驶载人飞船的成功发射和回收后，我国又已经成功发送了“神州二号”、“神州三号”、“神州四号”无人宇宙飞船。所了解，我国将要按计划发送首架载人航天飞船——“神州五号”上天。届时我国宇宙员将乘我国自行研制的载人飞船遨游太空。
（1）为了使飞船到达上述速度需要一个加速过程，在加速过程中，宇航员处于超重状态。人们把这种状态下宇航员对座椅的压力与静止在地球表面时的重力的比值称为耐受力值，用k表示。选择宇航员时，要求他在此状态下的耐受力值为4 ≤ k ≤ 12，试求飞船在竖直向上发射时的加速度值的变化范围；
（2）若飞船绕地球运行的轨道离地面高度为400km，已知地球半径为6400km，地球表面重力加速度g=10m/s²，求此飞船的速度。（保留2位有效数字）

有一质量为m的航天器靠近地球表面绕地球作圆周运动（轨道半径等于地球半径），某时刻航天器启动发动机，在很短的时间内动能变为原来的，此后轨道为椭圆，远地点与近地点距地心的距离之比是2：1，经过远地点和经过近地点的速度之比为1：2．己知地球半径为R，地球质量为M，万有引力恒量为G．
（1）求航天器靠近地球表面绕地球作圆周运动时的动能；
（2）在从近地点运动到远地点的过程中克服地球引力所做的功为多少?

要发射一颗人造地球卫星，使它在半径为r₂的预定轨道上绕地球做匀速圆周运动，为此先将卫星发射到半径为r₁的近地暂行轨道上绕地球做匀速圆周运动．如图10所示，在A点，使卫星速度增加，从而使卫星进入一个椭圆的转移轨道上，当卫星到达转移轨道的远地点B时，再次改变卫星速度，使它进入预定轨道运行，试求卫星从A点到B点所需的时间．已知地球表面的重力加速度大小为g，地球的半径为R．

(17分) 在“嫦娥探月”工程中，假设月球半径为R，月球表面的重力加速度为，飞船在半径为4R的圆形轨道Ⅰ运动，到达轨道的A点点火变轨进入椭圆轨道Ⅱ，到达轨道的近月点B再次点火进入月球近月轨道Ⅲ绕月球作圆周运动．求：

（1）飞船在轨道Ⅰ上的运行速率；
（2）飞船在A点处点火后瞬间与点火前相比，速度是变大还是变小？
（3）飞船在轨道Ⅲ绕月球运行一周所需的时间．

右图为某报纸的一篇科技报道，你能发现其中的科学性问题吗？请通过必要的计算加以说明。下面的数据在你需要时可选用。

引力常量G＝6.7×10^－11N·m²/kg²；地球表面重力加速度g＝10m/s²；地球半径R＝6.4×10⁶m；地球自转周期T＝8.6×10⁴s；地球公转周期T＇＝3.2×10⁷s。（π²＝10；70～80的立方根约取4.2）

神舟五号载人飞船在距地面高度为h的轨道上做匀速圆周运动，已知地球半径为R，地面附近的重力加速度大小为g，引力常量为G。试求：
（1）地球的质量M
（2）飞船在上述圆轨道上运行的周期T。