高中物理人造卫星计算题

图为中国月球探测工程的想象标志，它以中国书法的笔触，勾勒出一轮明月和一双踏在其上的脚印，象征着月球探测的终极梦想，我国自主研制的第一颗月球探测卫星“嫦娥一号”的发射成功,标志着我国实施绕月探测工程迈出重要一步。一位勤于思考的同学，为探月宇航员设计了如下实验：在距月球表面高h处以初速度v₀水平抛出一个物体，然后测量该平抛物体的水平位移为x，通过查阅资料知道月球的半径为R，引力常量为G，若物体只受月球引力的作用，请你求出：

（1）月球的质量；
（2）环绕月球表面的宇宙飞船的速率。

我国首个月球探测计划“嫦娥工程”将分三个阶段实施，大约用十年左右时间完成。物理老师要求同学用所学的知识，设计一个测量月球密度的方案，交给我国将来登月的宇航员来完成。某研究小组提出如下方案：我们现已知万有引力常数G和月球的半径R，假设月球为密度均匀的球体。只要让宇航员在月球表面上从H高度自由释放一个小球，求出它下落的时间t , 就可求出月球的密度，请你求出该小组用上述已知量和假想的实验量来表示月球密度的表达式。

有一颗绕地球做匀速圆周运动的卫星，到地心的距离为地球半径R₀的2倍，卫星圆形轨道平面与地球赤道平面重合。已知地球表面重力加速度为g，近似认为太阳光是平行光，试估算：
（1）卫星做匀速圆周运动的周期；
（2）卫星绕地球一周，太阳能收集板工作时间

一位同学为探月宇航员设计了如下实验:在距月球表面高h处以初速度v_o水平抛出一个物体,然后测量该平抛物体的水平位移为x,通过查阅资料知道月球的半径为R,引力常量为G,若物体只受月球引力的作用,求:
(1)月球表面的重力加速度
(2)月球的质量
(3)环绕月球表面运行的宇宙飞船的线速度

如图5－4－6，质量分别为m和M的两个星球A和B在引力作用下都绕O点做匀速圆周运动，星球A和B两者中心之间的距离为L.已知A、B的中心和O三点始终共线，A和B分别在O的两侧．引力常数为G.

图5－4－6
(1)求两星球做圆周运动的周期；
(2)在地月系统中，若忽略其他星球的影响．可以将月球和地球看成上述星球A和B，月球绕其轨道中心运行的周期记为T₁.但在近似处理问题时，常常认为月球是绕地心做圆周运动的，这样算得的运行周期记为T₂.已知地球和月球的质量分别为5.98×10²⁴ kg和7.35×10²² kg.求T₂与T₁两者平方之比．(结果保留3位小数)

如图所示，A是地球的同步卫星，另一卫星B的圆形轨道位于赤道平面内，离地面高度为h，已知地球半径为R，地球自转角速度为，地球表面的重力加速度为g，O为地球中心．
（1）求卫星B的运行周期；
（2）如果卫星B绕行方向与地球自转方向相同，某时刻A、B两卫星相距最近（O、B、A在同一直线上），则至少经过多长时间，它们再一次相距最近？

a、b两颗卫星在同一轨道平面内绕地球作匀速圆周运动，地球半径为R，a 卫星离地面高度为R，b卫星离地面高度为3R，则a、b两卫星周期之比为多大？若某时刻两卫星正好同时通过地面上同一点的正上方，a卫星至少经过多少个周期两卫星相距最远？

2005年10月12日9时，“神舟”六号飞船一飞冲天，一举成功，再次把中国人“巡天遥看一天河”的陆地梦想变成“手可摘星辰，揽明月”的太空现实，“神舟”六号飞船点火发射时，飞船处于一个加速过程，在加速过程中宇航员处于超重状态。人们把这种状态下宇航员所受支持力F_N与在地表面时重力mg的比值称为载荷值。
（1）假设宇航员聂海胜和费俊龙在超重状态下载荷值的最大值为K=7，飞船带着宇航员竖直向上发射时的加速度a的最大值为多少？已知地球表面的重力加速度g=10m/s²。
（2）“神舟”六号飞船发射成功后，进入圆形轨道稳定运行，运转一圈的时间为T，地球的半径为R，表面的重力加速度为g，万有引力常量为G，试求这一圆形轨道距离地面的 高度H。（用R、g、T、G表示）

已知地球半径为R，地球表面重力加速度为g，不考虑地球自转的影响。
（1）推导第一宇宙速度v₁的表达式；
（2）若卫星绕地球做匀速圆周运动，运行轨道距离地面高度为h，求卫星的运行周期T。

(12分)我国首个月球探测计划“嫦娥工程”将分三个阶段实施，大约用十年左右时间完成，这极大的提高了同学们对月球的关注程度。以下是某同学就有关月球的知识设计的两个问题，请你解答：
⑴若已知地球半径为R，地球表面的重力加速度为g，月球绕地球运动的周期为T，且把月球绕地球的运动近似看做是匀速圆周运动。试求出月球绕地球运动的轨道半径。
⑵若某位宇航员随登月飞船登陆月球后，在月球表面某处以速度v₀竖直向上抛出一个小球，经过时间t，小球落回到抛出点。已知月球半径为R_月，万有引力常量为G。试求出月球的质量M_月。

我国在2011年10月24日发射第二颗月球卫星——“嫦娥二号”．同学们也对月球有了更多的关注．
⑴若已知地球半径为R，地球表面的重力加速度为g，月球绕地球运动的周期为T，月球绕地球的运动近似看做匀速圆周运动，试求出月球绕地球运动的轨道半径r；
⑵若宇航员随登月飞船登陆月球后，在月球表面某处以速度v₀ 竖直向上抛出一个小球，经过时间t，小球落回抛出点．已知月球半径为R_月，万有引力常量为G ，试求出月球的质量M_月．

“神州六号”飞船的成功飞行为我国在2010年实现探月计划——“嫦娥工程”获得了宝贵的经验。如图所示，假设月球半径为R，月球表面的重力加速度为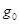，飞船在距月球表面高度为3R的圆形轨道Ⅰ运动，到达轨道的A点点火变轨进入椭圆轨道Ⅱ，到达轨道的近月点B再次点火进入月球近月轨道Ⅲ绕月球作圆周运动。求：

⑴飞船在轨道Ⅰ上的运行速率；
⑵飞船在轨道Ⅲ绕月球运行一周所需的时间。

随着航天技术的不断发展，人类宇航员可以乘航天器登陆一些未知星球。一名宇航员在登陆某星球后为了测量此星球的质量进行了如下实验：他把一小钢球托举到距星球表面高度为h处由静止释放，计时仪器测得小钢球从释放到落回星球表面的时间为t。此前通过天文观测测得此星球的半径为R，已知万有引力常量为G，不计小钢球下落过程中的气体阻力，可认为此星球表面的物体受到的重力等于物体与星球之间的万有引力。求：
(1）此星球表面的重力加速度g；
(2）此星球的质量M；
(3）若距此星球表面高H的圆形轨道有一颗卫星绕它做匀速圆周运动，求卫星的运行周期T。

“嫦娥奔月”是中国家喻户晓的神话故事，我国于2004年制定了“嫦娥工程”。继“嫦娥一号”和“嫦娥二号”卫星成功发射后，2012年3月13日，国家科防局发布消息，中国探月工程二期“嫦娥三号”任务已正式由初样研制转入正样研制阶段，计划于2013年发射。嫦娥三号任务是探月工程二期的关键任务，将突破月球软着陆、月面巡视勘察、月面生存、深空测控通信与遥操作（如图15），将是我国首次实现在地外天体上的软着陆。这极大地提高了同学们对月球的关注程度，以下是某同学就有关月球的知识设计的两个问题，请你解答：

（1）若已知地球半径为R，地球表面的重力加速度为，月球绕地球运动的周期为，且把月球绕地球的运动近似看作是匀速圆周运动。试求出月球绕地球运动的轨道半径
（2）若某位宇航员随登月飞船登陆月球后，在月球某水平表面上方高处以速度水平ν₀抛出一个小球，小球落回到月球表面的水平距离为。已知月球半径为，万有引力常量为。试求出月球的质量。

2008年9月，神舟七号载人航天飞行获得了圆满成功，我国航天员首次成功实施空间出舱活动、飞船首次成功实施释放小伴星的实验，实现了我国空间技术发展的重大跨越．已知飞船在地球上空的圆轨道上运行时离地面的高度为h．地球半径为R，地球表面的重力加速度为g．求飞船在该圆轨道上运行时：
（1）速度v的大小；
（2）速度v与地球第一宇宙速度的比值。