已知地球半径为6.4×106 m,又知月球绕地球的运动可近似看作匀速圆周运动,则可估算出月球到地心的距离为________________m(结果只保留一位有效数字).
设想人类开发月球,不断把月球上的矿藏搬运到地球上,假定经过长时间开采后,月球仍可看作是均匀的球体,月球仍沿开采前的圆周轨道运动,则与开采前相比( )
| A.地球与月球间的万有引力将变大 |
| B.地球与月球间的万有引力将变小 |
| C.月球绕地球运动的周期将变长 |
| D.月球绕地球运动的周期将变短 |
若已知行星绕太阳公转的半径为r,公转的周期为T,万有引力常量为G,则可求出( )
| A.某行星的质量 |
| B.太阳的质量 |
| C.某行星的密度 |
| D.太阳的密度 |
在研究宇宙发展演变的理论中,有一种学说叫“宇宙膨胀说”,这种学说认为引力常量G在缓慢地减小.根据这一理论,在很久很久以前,太阳系中地球的公转情况与现在相比( )
| A.公转半径R较大 | B.公转周期T较小 |
| C.公转速率v较大 | D.公转角速度ω较小 |
美国“勇气”号和“机遇”号火星车分别登陆火星,同时欧洲的“火星快车”探测器也在环火星轨道上开展了大量科学探测活动。科学家们根据探测器返回的数据进行分析,推测火星表面存在大气,且大气压约为地球表面大气压的1/200,火星直径约为地球的一半,地球的平均密度ρ地=5.5×103kg/m3,火星的平均密度ρ火=4.0×103kg/m3。请根据以上数据估算火星大气质量是地球大气质量的多少倍?(地球和火星表面大气层的厚度均远远小于球体的半径,结果保留两位有效数字)
地球和月球的质量之比为81:1,半径之比4:1,求:
(1)地球和月球表面的重力加速度之比;
(2)在地球上和月球上发射卫星所需最小速度之比.
已知引力常量为G,地球的质量为M,地球的半径为R,某飞船绕地球做匀速圆周运动时距地面的高度为h。根据以上条件求(用题中字母表示结果):
(1)该飞船绕地球做匀速圆周运动时的轨道半径;
(2)该飞船绕地球做匀速圆周运动时的线速度大小。
已知国际空间离地高度为H,绕地球运动的周期为T1,万有引力常量为G,地球半径为R,地球同步卫星距地面的高度为h,地球的自转周期为T2,地球表面重力加速度为g。
某同学根据以上条件,提出一种估算地球质量M的方法:
地球同步卫星绕地心做圆周运动,由牛顿第二定律得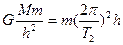
解得: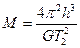
(1)这个同学的解题过程存在错误,请指出错误之处,并给出正确解法。
(2)请根据题给条件再提出一种估算地球质量的方法,并解得结果。
神舟六号飞船2005年10月12日9时在酒泉发射场升空,在太空环绕地球五天后,按预定的程序平稳地在内蒙古中部着陆。若将飞船环绕地球的运动看作匀速圆周运动时距地面的高度为h,绕地球一周的时间为T,地球半径为R。引力常量为G。
求
(1)飞船在环绕地球做圆周运动的加速度大小
(2)地球的质量
星体对它们的引力作用) .设四颗星稳定地分布在边长为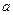 的正方形的四令顶点上且
的正方形的四令顶点上且
它们均围绕正方形对角线的交点做匀速圆周运动,星体运动周期为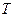 ,每个星体表面
,每个星体表面
的重力加速度为g,引力常量为G,试求:每个星体的半径和质量.
如图所示,A、B两行星在同一平面内绕同一颗恒星运动,运动的方向相同,A、B两行星的轨道半径分别为r1、r2,已知恒星的质量为M,且恒星对两行星的引力远远大于两行星间的引力,两行星的轨道半径r1<r2,若在某一时刻两行星相距最近,试求:
(1)经多长时间两行星相距最近?
(2)经多长时间两行星相距最远?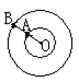
(1)火星的第一宇宙速度是多少?
(2)火星表面附近的重力加速度g是多少?
(3)若你的质量是m、秋千的绳长l、绳与竖直方向的最大夹角等于θ,求你经过最低点的速度大小?
已知万有引力常量为G,地球半径为R,同步卫星距地面的高度为h,地球的自转周期为T,地球表面的重力加速度为g。某同学根据以上条件,提出一种估算地球赤道表面的物体随地球自转的线速度大小的方法:
地球赤道表面的物体随地球作圆周运动,由牛顿运动定律有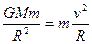
又因为地球上的物体的重力约等于万有引力,有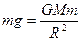
由以上两式得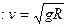
(1)请判断上面的结果是否正确?
(2)由题目给出的条件还可以估算出哪些物理量?
(1)岩石颗粒A和B的线速度之比(2)岩石颗粒A和B的周期之比
(3)土星探测器上有一物体,在地球上重为10 N,推算出他在距土星中心3.2×105 km处受到土星的引力为0.38 N。已知地球半径为6.4×103 km,请估算土星质量是地球质量的多少倍?