已知下面的哪组数据,可以算出地球的质量M地(引力常量G已知)( )
| A.月球绕地球运行的周期T及月球到地球中心的距离R1 |
| B.地球绕太阳运行的周期T2及地球到太阳中心的距离R2 |
| C.人造卫星在地面附近的运行速度v3和运行周期T3 |
| D.地球绕太阳运行的速度v4及地球到太阳中心的距离R4 |
行星绕太阳的运动可以近似看作是匀速圆周运动,万有引力就是向心力,关于行星所受向心力和轨道半径的关系,下列说法正确的是( )
A.根据F=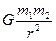 可知,向心力与r2成反比 可知,向心力与r2成反比 |
B.根据F=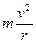 可知,向心力与r成反比 可知,向心力与r成反比 |
| C.根据F=mω2r可知,向心力与r成正比 |
| D.根据F=mωv可知,向心力与r无关 |
如果把地球绕太阳公转看作是匀速圆周运动,轨道平均半径约为1.5×108 km,已知万有引力常量G=6.67×10-11N·m2/kg2,则可估算出太阳的质量大约是多少?(结果取一位有效数字)
土星周围有美丽壮观的“光环”,组成环的颗粒是大小不等.线度从1 μm到10 m的岩石、尘埃,类似于卫星,它们与土星中心的距离从7.3×104km延伸到1.4×105km.已知环的外缘颗粒绕土星做圆周运动的周期约为14 h,引力常量为6.67×10-11 N·m2/kg2,则土星的质量约为(估算时不考虑环中颗粒间的相互作用)( )
| A.9.0×1016kg | B.6.4×1017kg |
| C.9.0×1025kg | D.6.4×1026kg |
一太空探测器进入了一个圆形轨道绕太阳运转,已知其轨道半径为地球绕太阳运转轨道半径的9倍,则太空探测器绕太阳运转的周期是( )
| A.3年 |
| B.9年 |
| C.27年 |
| D.81年 |
两行星A和B是两均匀球体,行星A的卫星A沿圆轨道运行的周期为Ta,行星B的卫星B沿圆轨道运行的周期为Tb.设两卫星均为各自中心星体的近地卫星.而且Ta∶Tb=1∶4,行星A和行星B的半径之比RA∶RB=1∶2,则行星A和行星B的密度之比ρA∶ρB=___________,行星表面的重力加速度之比gA∶gB=___________.
两个行星质量分别为m1和m2,绕太阳运行的轨道半径分别是r1和r2,求:
(1)它们与太阳间的万有引力之比;
(2)它们的公转周期之比.
如果万有引力定律表达式中,两质点之间的引力大小与其距离的n次方(n≠2)成反比,考虑一群以圆形轨道绕同一恒星运动的行星(行星间的引力不计),设各行星的周期与其轨道半径的平方成正比,则n的值为_______________.
下列有关行星运动的说法中,正确的是( )
A.由ω=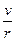 知,行星轨道半径越大,角速度越小 知,行星轨道半径越大,角速度越小 |
| B.由a=rω2知,行星轨道半径越大,行星的加速度越大 |
C.由a=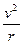 知,行星轨道半径越大,行星的加速度越小 知,行星轨道半径越大,行星的加速度越小 |
D.由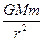 =m =m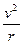 知,行星的轨道半径越大,线速度越小 知,行星的轨道半径越大,线速度越小 |
关于万有引力定律应用于天文学研究的历史事实,下列说法中正确的是( )
| A.天王星、海王星和冥王星都是运用万有引力定律,经过大量计算以后而发现的 |
| B.在18世纪已发现的7个行星中,人们发现第七颗行星——天王星的运动轨道总是同根据万有引力定律计算出来的理论轨道有较大的偏差,于是有人推测,在天王星轨道之外还有一个行星,是它的存在引起了上述偏差 |
| C.海王星是牛顿运用了万有引力定律经过大量计算而发现的 |
| D.冥王星是英国剑桥大学的学生亚当斯和勒维列合作研究后共同发现的 |
利用下列哪组数据,可以计算出地球的质量( )
| A.地球的半径R地和地面的重力加速度g |
B.卫星绕地球做匀速圆周运动的半径R和周期T |
C.卫星绕地球做匀速圆周运动的半径R和线速度v |
D.卫星绕地球做匀速圆周运动的线速度v和周期T |