2013年6月我国宇航员在天宫一号空间站中进行了我国首次太空授课活动,其中演示了太空“质量测量仪”测质量的实验,助教聂海胜将自己固定在支架一端,王亚平将连接运动机构的弹簧拉到指定位置,如图所示;松手后,弹簧凸轮机构产生恒定的作用力,使弹簧回到初始位置,同时用光栅测速装置测量出支架复位时的速度和所用时间;这样,就测出了聂海胜的质量为74kg;下列关于“质量测量仪”测质量的说法正确的是( )

| A.测量时仪器必须水平放置 | B.其测量原理根据牛顿第二定律 |
| C.其测量原理根据万有引力定律 | D.测量时仪器必须竖直放置 |
如图所示,有一个质量为M,半径为R,密度均匀的大球体。从中挖去一个半径为的小球体,并在空腔中心放置一质量为m的质点,则大球体的剩余部分对该质点的万有引力大小为(已知质量分布均匀的球壳对壳内物体的引力为零)
| A.0 | B. |
C. |
D. |
某宇航员在一星球表面附近高度为H处以速度v0水平抛出一物体,经过一段时间后物体落回星球表面,测得该物体水平位移为x,已知星球半径为R,万有引力常量为G.不计空气阻力,求:
(1)该星球质量M;
(2)该星球第一宇宙速度大小v.
设地球半径为R,a为静止在地球赤道上的一个物体,b为一颗近地绕地球做匀速圆周运动的人造卫星,c为地球的一颗同步卫星,其轨道半径为r。下列说法中正确的是( )
A.a与c的线速度大小之比为 |
B.a与c的线速度大小之比为 |
C.b与c的周期之比为 |
D.b与c的周期之比为  |
如图所示,双星系统中的星球A、B都可视为质点,A、B绕两者连线上的O点做匀速圆周运动,A、B之间距离不变,引力常量为G,观测到A的速率为v、运行周期为T,A、B的质量分别为mA、mB.
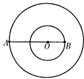
(1)求B的周期和速率.
(2)A受B的引力FA可等效为位于O点处质量为m′的星体对它的引力,试求m′.(用mA、mB表示)( )
由于地球自转的影响,地球表面的重力加速度会随纬度的变化而有所不同:若地球表面两极处的重力加速度大小为g0,在赤道处的重力加速度大小为g,地球自转的周期为r,引力常量为G,地球可视为质量均匀分布的球体.求:
(1)地球半径R;
(2)地球的平均密度;
(3)若地球自转速度加快,当赤道上的物体恰好能“飘”起来时,求地球自转周期T'.
“轨道康复者”是“垃圾”卫星的救星,被称为“太空110”,它可在太空中给“垃圾”卫星补充能源,延长卫星的使用寿命,假设“轨道康复者”的轨道半经为地球同步卫星轨道半径的五分之一,其运动方向与地球自转方向一致,轨道平面与地球赤道平面重合,下列说法正确的是( )
| A.“轨道康复者”的加速度是地球同步卫星加速度的25倍 |
B.“轨道康复者”的速度是地球同步卫星速度的 倍 倍 |
| C.站在赤道上的人观察到“轨道康复者”向西运动 |
| D.“轨道康复者”可在高轨道上加速,以实现对低轨道上卫星的拯救 |
同步卫星轨道半径为r,运行速率为v1,加速度为a1;地球赤道上的物体随地球自转的向心加速度为a2;第一宇宙速度为v2;地球半径为R.则下列关系式正确的是( )
A. = = |
B. =( =( )2 )2 |
C. = = |
D. = = |
已知引力常量G和下列备组数据,不能计算出地球质量的是( )
| A.地球绕太阳运行的周期及地球离太阳的距离 |
| B.月球绕地球运行的周期及月球离地球的距离 |
| C.人造卫星在地面附近绕行的速度和运行周期 |
| D.若不考虑地球自转,已知地球的半径及重力加速度 |
“轨道康复号”是“垃圾卫星”的救星,它可在太空中给“垃圾卫星”补充能量,延长卫星的使用寿命。一颗“轨道康复号”正在地球赤道平面内的圆周轨道上运行,运行方向与地球自转方向一致。轨道半径为地球同步卫星轨道半径的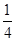 ,则
,则
| A.“轨道康复号”相对于地球赤道上的城市向西运动 |
| B.“轨道康复号”的加速度是地球同步卫星加速度的4倍 |
C.“轨道康复号”的周期是地球同步卫星周期的 倍 倍 |
D.“轨道康复号”每经过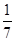 天就会再赤道同一城市的正上方出现 天就会再赤道同一城市的正上方出现 |
太阳系中的九大行星绕太阳公转的轨道均可视为圆,不同行星的轨道平面均可视为同一平面。如图所示,当地球外侧的行星运动到日地连线上,且和地球位于太阳同侧时,与地球的距离最近,我们把这种相距最近的状态称为行星与地球的“会面”。若每过N1年,木星与地球“会面”一次,每过N2年,天王星与地球“会面”一次,则木星与天王星的公转轨道半径之比为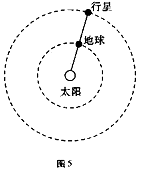
A. |
B.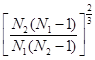 |
C. |
D.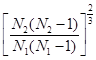 |
1798年英国物理学家卡文迪许测出万有引力常量G,因此卡文迪许被人们称为能称出地球质量的人,若已知万有引力常量G,地球表面处的重力加速度g,地球半径为R,地球上一个昼夜的时间为T1(地球自转周期),一年的时间T2(地球公转的周期),地球中心到月球中心的距离L1,地球中心到太阳中心的距离为L2.你可估算出( )
A.地球的质量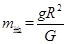 |
B.太阳的质量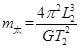 |
C.月球的质量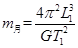 |
D.可求月球、地球及太阳的密度 |
下列说法正确的是( )
| A.丹麦天文学家第谷通过长期的天文观测,指出所有行星绕太阳运动的轨道都是椭圆,揭示了行星运动的有关规律 |
| B.卫星轨道必为圆形,卫星运行速度总不超过7.9km/s |
| C.卫星运行速度与卫星质量无关 |
| D.卫星轨道可以与纬度不为零的某条纬线在同一平面内 |
黑洞是近代引力理论所预言的一种特殊天体,探寻黑洞的方案之一是观测双星系统的运动规律.天文学家观测河外星系大麦哲伦云时,发现了LMCX-3双星系统,它由可见星A和不可见的暗星B构成。两星视为质点,不考虑其它天体的影响,A、B围绕两者连线上的O点做匀速圆周运动,它们之间的距离保持不变,如图所示。引力常量为G,由观测能够得到可见星A的速率v和运行周期T。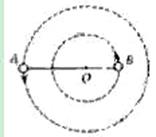
(1)可见星A所受暗星B的引力 可等效为位于O点处质量为
可等效为位于O点处质量为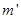 的星体(视为质点)对它的引力,设A和B的质量分别为
的星体(视为质点)对它的引力,设A和B的质量分别为 、
、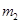 ,试求
,试求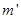 (用
(用 、
、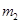 表示);
表示);
(2)求暗星B的质量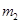 与可见星A的速率v、运行周期T和质量
与可见星A的速率v、运行周期T和质量 之间的关系式;
之间的关系式;
(3)恒星演化到末期,如果其质量大于太阳质量 的2倍,它将有可能成为黑洞。若可见星A的速率v=2.7×105m/s,运行周期T=4.7π×104s,质量m1=6
的2倍,它将有可能成为黑洞。若可见星A的速率v=2.7×105m/s,运行周期T=4.7π×104s,质量m1=6 ,试通过估算来判断暗星B有可能是黑洞吗?(G=6.67×10-11N·m2/kg2,ms=2.0×1030kg)
,试通过估算来判断暗星B有可能是黑洞吗?(G=6.67×10-11N·m2/kg2,ms=2.0×1030kg)