我国探月的“嫦娥工程”已启动，在不久的将来，我国宇航员将登上月球。假如宇航员在月球上测得摆长为L的单摆做小振幅振动的周期为T，将月球视为密度均匀、半径为r的球体，则月球的密度为( )
A． |
B． |
C． |
D． |
一艘宇宙飞船在一个星球表面附近，沿着圆形轨道，环绕该星球作近地飞行。若要估测该星球的平均密度，则该宇航员只需要测定的一个参量是： （ ）
| A．飞船的环绕半径 | B．行星的质量 |
| C．飞船的环绕周期 | D．飞船的环绕速度 |
在万有引力定律发现过程中，牛顿曾经做过著名的“月—地”检验，他设想：如果地球对月球的引力和对地表附近物体的引力性质相同，已知月地间距离为地球半径的60倍，地球表面的重力加速度为g ,那么月球绕地球公转的加速度应该为（ ）
A． |
B．60 |
C． |
D． |
2003年8月29日，火星、地球和太阳处于三点一线，上演“火星冲日”的天象奇观．这是6万年来火星距地球最近的一次，与地球之间的距离只有5576万公里，为人类研究火星提供了最佳时机．图示为美国宇航局最新公布的“火星冲日”的虚拟图．则下列说法错误的是（ ）
| A．2003年8月29日，火星的线速度小于地球的线速度 |
| B．2003年8月29日，火星的角速度小于地球的角速度 |
| C．2004年8月29日，火星还没有回到该位置 |
| D．2004年8月29日，火星又回到该位置 |
随着太空技术的飞速发展，地球上的人们登陆其它星球成为可能。假设未来的某一天，宇航员登上某一星球后，测得该星球表面的重力加速度是地球表面重力加速度的2倍，而该星球的平均密度与地球的差不多，则该星球质量大约是地球质量的（ ）
| A．0.5倍 | B．2倍 | C．4倍 | D．8倍 |
两个质点相距r时，它们之间的万有引力为F，若它们间的距离缩短为1/2r，其中一个质点的质量变为原来的2倍，则它们之间的万有引力为（ ）
| A．2F | B．4F | C．8F | D．16F |
宇宙飞船在受到星球的引力作用时，宇宙飞船的引力势能大小的表达式为
，式中R为此星球球心到飞船的距离，M为星球的质量，m为宇宙飞船的质量，G为万有引力恒量。现有一质量m=104kg的宇宙飞船从地球表面飞到月球，则：
（1）写出宇宙飞船在地球表面时的引力势能表达式（不要计算出数值，地球质量为
、月球质量为
）。
（2）宇宙飞船在整个飞行过程中至少需做多少功？
已知月球表面重力加速度为地球表面重力加速度的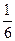
，地球半径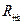
=6.4×106m，月球半径
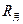=1.7×106m，月球到地球距离
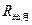=3.8×108m（提示：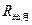
，）。
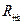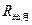
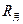某宇航员在飞船发射前测得自身连同宇航服等装备共重840N，在火箭发射阶段，发现当飞船随火箭以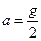
的加速度匀加速竖直上升到某位置时（其中g为地面处的重力加速度），其身下体重测试仪的示数为1220N。设地球半径R=6400km，地球表面重力加速度g=10m/s2（求解过程中可能用到
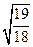=1.03，
=1.02）。问：
（1）该位置处的重力加速度g′是地面处重力加速度g的多少倍？
（2）该位置距地球表面的高度h为多大？
宇航员在地球表面以一定初速度v0竖直上抛一小球，经过时间t小球落回原处；若他在某星球表面以相同的初速度v0竖直上抛同一小球，需经过时间5t小球落回原处。（取地球表面重力加速度g＝10 m/s2，空气阻力不计）
（1）求该星球表面附近的重力加速度g/；
（2）已知该星球的半径与地球半径之比为R星:R地＝1:4，求该星球与地球质量之比M星:M地和两星球第一宇宙速度之比V星:V地
两艘质量各为1×107kg的轮船相距100m时，万有引力常量G=6.67×10-11N·m2/kg2,它们之间的万有引力相当于：
| A．一个人的重量级 | B．一只鸡蛋的重量级 |
| C．一个西瓜的重量级 | D．一头牛的重量级 |
在研究宇宙发展演变的理论中，有一种学说叫做“宇宙膨胀说”，这种学说认为引力常量G在缓慢地减小。假设月球绕地球做匀速圆周运动，且它们的质量始终保持不变，根据这种学说当前月球绕地球做匀速圆周运动的情况与很久很久以前相比
| A．周期变大 | B．角速度变大 | C．轨道半径减小 | D．速度变大 |
某行星绕太阳运动可近似看作匀速圆周运动，已知行星运动的轨道半径为，周期为
，万有引力恒量为
，则该行星的线速度大小为；太阳的质量可表示为。
，求出“风云二号”D气象卫星的轨道半径r；
粤公网安备 44130202000953号