高中物理万有引力定律及其应用计算题

若已知某行星的质量为m，该行星绕太阳公转的半径为r，公转周期为T，万有引力常量为G，则由此求出：该行星绕太阳公转的角速度ω太阳的质量M

某物体质量为50kg，将它放置在卫星中的台秤上，当卫星以的加速度随火箭向上加速升空的过程中，某时刻发现台秤的示数为350N，此时卫星距离地球表面有多远？已知地球半经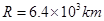，地球表面的重力加速度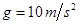。（计算结果保留三位有效数字）

某宇航员在地面上体重为600N，他在宇宙飞船中以5m/s²的加速度竖直匀加速上升，当上升到某高度时他所受的支持力为450N，求：①、宇航员的质量；②、此时宇宙飞船离地面的高度。（取地球半径6.4×10³km，地球表面处重力加速度10m/s²）

在“北斗”卫星导航系统中，同步卫星起到非常重要的作用，这些卫星运动在离地心的距离为r的圆形轨道上。已知某颗同步卫星的质量m，引力常量G，地球自转周期为T，请根据以上信息，求出下列物理量（用题中给出的物理量表示）。求：（1）同步卫星运动的角速度大小；
（2）地球对该卫星的吸引力大小；
（3）地球的质量大小。

一颗质量为m的人造地球卫星绕地球做匀速圆周运动，卫星到地心的距离为r，已知引力常量G、地球质量M和地球半径R，求：
（1）地球对卫星的万有引力的大小；
（2）卫星的速度大小；
（3）地球表面重力加速度（不考虑地球自转）。

已知地球半径为R，地球表面重力加速度为g，万有引力常量为G，不考虑地球自转的影响．
（1）求地球的质量M?
（2）求地球的第一宇宙速度v?
（3）若卫星绕地球做匀速圆周运动且运行周期为T，求卫星距离地面的高度h.

已知万有引力常量G，地球半径R₁，地球和太阳之间的距离r₁，地球绕太阳公转的周期T₁，月球半径R₂，地球和月亮之间的距离r₂，月球绕地球公转的周期T₂，地球表面的重力加速度g。请根据已知条件用二种估算方法地球的质量M。

在宇宙探索中，科学家发现某颗行星的质量和半径均为地球的1/2，宇航员登陆到该行星的表面时，将长度L=0.45m的细绳一端固定，另一端系质量m=0.1kg的金属球，并让金属球恰好能在竖直面内作圆周运动。已知地球表面重力加速度g=10m/s²。求：
⑴该行星表面的重力加速度g′；
⑵金属球通过最高点时线速度大小；
⑶金属球通过最低点时线速度大小

已知引力常量为G，地球的质量为M，地球的半径为R，某飞船绕地球做匀速圆周运动时距地面的高度为h.根据以上条件，试求该飞船绕地球做匀速圆周运动时的线速度大小？（用题中字母表示结果）

宇航员站在一质量分布均匀星球表面上某高h处，沿水平方向抛出一个小球．测得落地时间为t．该星球的半径为R，万有引力常量为G，求
(1)该星球的质量M．
(2)该星球的密度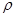
(3)该星球的第一宇宙速度

某人造地球卫星沿圆轨道运行，轨道半径是r，周期是T。试根据这些量推导出计算地球质量M的表达式。（引力常量为G）

某宇航员在一星球表面附近高度为H处以速度v₀水平抛出一物体，经过一段时间后物体落回星球表面，，测得该物体的水平位移为x，已知星球半径为R，万有引力常量为G。不计空气阻力，求（1）该星球的质量（2）该星球的第一宇宙速度大小

太阳围绕银河系中心的运动可视为匀速圆周运动，其运动速度约为地球公转速度的7倍，轨道半径约为地球公转道半径的2×10⁹倍，为了粗略估算银河系中恒星的数目，可认为银河系中所有恒星的质量都集中在银河系中心，且银河系中恒星的平均质量约等于太阳质量，则银河系中恒星数目约为

A．10^9

B．10^11

C．10^13

D．10^15

通过天文观测发现某行星的卫星运动的周期为T，轨道半径为r，若把卫星的运动近似看成匀速圆周运动，行星的半径为Ｒ，试求出该行星的质量和密度。（万有引力常量G已知）

已知太阳的质量M＝2.0×10³⁰ kg，地球的质量m＝6.0×10²⁴ kg，太阳与地球相距r＝1.5×10¹¹ m，求太阳对地球的引力以及地球对太阳的引力．（G＝6.67×10^－11N·m²/kg2）