伽利略”木星探测器，从1989年10月进入太空起，历经6年，行程37亿千米，终于到达木星周围。此后在t秒内绕木星运行N圈后，对木星及其卫星进行考察，最后坠入木星大气层烧毁。设这N圈都是绕木星在同一个圆周上运行，其运行速率为V，探测器上的照相机正对木星拍摄到整个木星时的视角为θ（如图所示），设木星为一球体。求：
（1）木星探测器在上述圆形轨道上运行时的轨道半径；
（2）若人类能在木星表面着陆，至少以多大的速度将物体从其表面水平抛出，才不至于使物体再落回木星表面。
宇航员站在某一星球表面上的某高处，沿水平方向抛出一小球。经过时间t，小球落到星球表面，测得抛出点与落地点之间的距离为L。若抛出时的初速度增大到2倍，则抛出点与落地点之间的距离为
L。已知两落地点在同一水平面上，该星球的半径为R，万有引力常数为G。求该星球的质量M。
“嫦娥二号”卫星送入近地点高度200公里、远地点高度38万公里的直接奔月轨道，如图甲所示．卫星奔月飞行约需112小时；当卫星到达月球附近的特定位置时，实施近月制动，进入近月点100公里的椭圆轨道．再经过两次轨道调整，进入100公里的极月圆轨道．
(1)若运载“嫦娥二号”卫星的长征三号丙运载火箭点火后前300 s竖直向上运动的速度图象如图乙所示，前120s火箭的图线可以视为直线．假设在该高度地球对卫星的引力与地面时相同，地面重力加速度g＝10 m/s2，不计空气阻力，求：100s时火箭的高度和火箭对“嫦娥二号”的推力(保留3位有效数字)．
(2)若月球质量为M，半径为r，月球表面的重力加速度为地球表面重力加速度g的
“嫦娥二号”卫星在极月圆轨道运行时距月球表面高度为h，忽略“嫦娥二号”卫星在极月圆轨道运行时受到其他星体的影响．求“嫦娥二号”卫星在极月圆轨道的运行周期．(用题给物理量字母表示)
月球与地球质量之比约为1：80，一般情况下，我们认为月球绕地球运动，其轨道可近似认为是圆周轨道，但有研究者提出，地球的质量并非远远大于月球质量，故可认为月球和地球可视为一个由两质点构成的双星系统，他们都围绕地球与月球连线上某点O做匀速圆周运动。在月地距离一定的情况下，试计算这种双星系统所计算出的周期T1与一般情况所计算出的周期T2之比。（结果可用根号表示）
我国在2010年实现探月计划——“嫦娥工程”。同学们也对月球有了更多的关注。
(1)若已知地球半径为R，地球表面的重力加速度为g，月球绕地球运动的轨道半径为
，月球绕地球的运动近似看成匀速圆周运动，试求出月球绕地球运动的周期T．
(2)若宇航员随登月飞船登陆月球后，在月球表面高h处由静止释放一个小球，经过时间
，小球落回地面．已知月球半径为R月，万有引力常量为G，试求出月球的质量M月。
2007年10月24日，我国成功地发射了“嫦娥一号”探月卫星。卫星进入地球轨道后还需要对卫星进行10次点火控制。前4次点火，让卫星不断变轨加速，当卫星加速到
的速度时进入地月转移轨道向月球飞去。后6次点火的主要作用是修正飞行方向和被月球捕获时的紧急刹车，最终把卫星送入离月面h=200km高的工作轨道（可视为匀速圆周运动）。已知地球质量是月球质量的81倍，
，卫星质量为2350kg，地球表面重力加速度
，引力恒量
。(结果保留一位有效数字）求：
(1)地球的质量。
(2)卫星从离开地球轨道进入地月转移轨道最终稳定在离月球表面h=200km的工作轨道上外力对它做了多少功？（忽略地球自转及月球绕地球公转的影响）
用天文望远镜长期观测，人们在宇宙中发现了许多双星系统，通过对它们的研究，使我们对宇宙中物质存在的形式和分布有了较深刻的认识，双星系统是由两个星体构成，其中每个星体的线度都小于两星体间的距离，一般双星系统距离其它星体很远，可以当做孤立系统处理，现根据对某一双星系统的光度学测量确定，该双星系统中每个星体的质量都是M，两者相距L，它们正围绕两者连线的中点做圆周运动。
（1）计算该双星系统的运动周期T计算。
（2）若实验上观测到的运动周期为T观测，且T观测：T计算=1：
(N>1)，为了解释T观测与T计算的不同，目前有一种流行的理论认为，在宇宙中可能存在一种望远镜观测不到的暗物质，作为一种简化模型，我们假定在这两个星体边线为直径的球体内均匀分布着暗物质，而不考虑其它暗物质的影响，试根据这一模型和上述观测结果确定该星系间这种暗物质的密度。
(8分)在一次宇宙探险活动中，发现一行星，经观测其半径为R，当飞船在接近行星表面的上空做匀速圆周运动时，周期为T飞船着陆后，宇航员用绳子拉着质量为m的仪器箱在平坦的“地面”上运动，已知拉力大小为F，拉力与水平面的夹角为
，箱子做匀速直线运动．（引力常量为G）求：
（1）行星的质量M；
（2）箱子与“地面”间的动摩擦因数
航天员在月球上做自由落体实验，将某物体由距离月球表面高h处由静止释放，经时间t落到月球表面，已知月球半径为R，万有引力常量为G。试求：
（1）月球表面处重力加速度g的大小；
（2）月球的质量
（3）飞船在月球表面附近绕月球做匀速圆周运动的速度大小。
(12分)如图为宇宙中有一个恒星系的示意图，A为该星系的一颗星，它绕中央恒星O运动轨道近似为圆，天文学家观测得到A行星运动的轨道半径为R，周期为T 
(1)中央恒星O的质量是多大?
(2)长期观测发现，A行星实际运动的轨道与圆轨道总存在一些偏离，且周期性地每隔t时间发生一次最大的偏离，天文学家认为形成这种现象的原因可能是A行星外侧还存在着一颗未知的行星B(假设其运行轨道与A在同一平面内，且与A的绕行方向相同)，它对A行星的万有引力引起A轨道的偏离．根据上述现象及假设，预测未知行星B绕中央恒星O运行轨道半径有多大?
如图所示，宇航员站在某质量分布均匀的星球表面斜坡上，从P点沿水平方向以初速度v0抛出一个小球，测得小球经时间t落到斜坡上另一点Q，斜面的倾角为α，已知该星球半径为R，万有引力常量为G，求：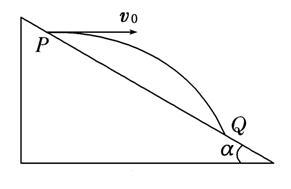
(1)该星球表面的重力加速度；
(2)该星球的第一宇宙速度v；
(3)该星球的密度。
一颗人造地球卫星在绕地球做匀速圆周运动，卫星距地面的高度是地球半径的15倍，即h=15R，试计算此卫星的线速度大小。已知地球半径R=6400km，地球表面重力加速度g=10m/s2.
某恒星远处有一颗行星，靠近行星周围有众多的卫星，且相对均匀地分布于行星周围。假设卫星绕行星的运动是匀速圆周运动，通过天文观测，测得离该行星最近的一颗卫星运动的轨道半径为
，周期为
。已知万有引力常量为G。
（1）求该行星的质量；
（2）通过天文观测，发现离该行星很远处还有一颗卫星，其运动的轨道半径为
，周期为
，试估算该行星周围众多卫星的总质量。
（3）通过天文观测发现，某一时刻行星跟距离自己最近的卫星以及距离自己很远的卫星正好分布在一条直线上，求再经过多长时间它们又将分布在一条直线上。
人们通过对月相的观测发现，当月球恰好是上弦月时，如图甲所示，人们的视线方向与太阳光照射月球的方向正好是垂直的，测出地球与太阳的连线和地球与月球的连线之间的夹角为θ.当月球正好是满月时，如图乙所示，太阳、地球、月球大致在一条直线上且地球在太阳和月球之间，这时人们看到的月球和在白天看到的太阳一样大(从物体两端引出的光线在人眼光心处所成的夹角叫做视角，物体在视网膜上所成像的大小决定于视角)．已知嫦娥飞船贴近月球表面做匀速圆周运动的周期为T，月球表面的重力加速度为g0，试估算太阳的半径．
已知月球的质量是地球质量的
，月球半径是地球半径的
，在月球表面16m处让质量m=50kg的物体自由下落，（已知地球表面的重力加速度g=10m/s2）。求：
（1）月球表面的重力加速度
是多大？
（2）物体下落到月球表面所用的时间t是多少？
（3）月球的第一宇宙速度是地球的第一宇宙速度的多少倍？
粤公网安备 44130202000953号