某恒星远处有一颗行星,靠近行星周围有众多的卫星,且相对均匀地分布于行星周围。假设卫星绕行星的运动是匀速圆周运动,通过天文观测,测得离该行星最近的一颗卫星运动的轨道半径为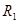 ,周期为
,周期为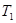 。已知万有引力常量为G。
。已知万有引力常量为G。
(1)求该行星的质量;
(2)通过天文观测,发现离该行星很远处还有一颗卫星,其运动的轨道半径为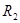 ,周期为
,周期为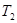 ,试估算该行星周围众多卫星的总质量。
,试估算该行星周围众多卫星的总质量。
(3)通过天文观测发现,某一时刻行星跟距离自己最近的卫星以及距离自己很远的卫星正好分布在一条直线上,求再经过多长时间它们又将分布在一条直线上。
某恒星远处有一颗行星,靠近行星周围有众多的卫星,且相对均匀地分布于行星周围。假设卫星绕行星的运动是匀速圆周运动,通过天文观测,测得离该行星最近的一颗卫星运动的轨道半径为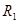 ,周期为
,周期为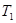 。已知万有引力常量为G。
。已知万有引力常量为G。
(1)求该行星的质量;
(2)通过天文观测,发现离该行星很远处还有一颗卫星,其运动的轨道半径为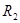 ,周期为
,周期为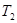 ,试估算该行星周围众多卫星的总质量。
,试估算该行星周围众多卫星的总质量。
(3)通过天文观测发现,某一时刻行星跟距离自己最近的卫星以及距离自己很远的卫星正好分布在一条直线上,求再经过多长时间它们又将分布在一条直线上。