为了迎接太空时代的到来,美国国会通过一项计划:在2050年前建造成太空升降机,就是把长绳的一端搁置在地球的卫星上,另一端系住长降机。放开绳,升降机能到达地球上;人坐在升降机里,在卫星上通过电动机把升降机拉到卫星上。已知地球表面的重力加速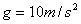 ,地球半径为
,地球半径为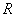 。求:
。求:
(1)某人在地球表面用体重计称得重180N,站在升降机中,当升降机以加速度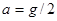 (
(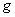 为地球表面处的重力加速度)竖直上升时,在某处此人再一次用同一体重计称得视重为170N,忽略地球自转的影响,求升降机此时距地面的高度;
为地球表面处的重力加速度)竖直上升时,在某处此人再一次用同一体重计称得视重为170N,忽略地球自转的影响,求升降机此时距地面的高度;
(2)如果把绳的一端搁置在同步卫星上,地球自转的周期为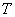 ,求绳的长度至少为多长。
,求绳的长度至少为多长。
我国首个月球探测计划“嫦娥工程”将分三个阶段实施,大约用十年左右时间完成,这极大地提高了同学们对月球的关注程度.以下是某同学就有关月球的知识设计的问题,请你解答:若已知地球半径为 ,地球表面的重力加速度为
,地球表面的重力加速度为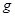 ,月球绕地球运动的周期为
,月球绕地球运动的周期为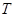 ,且把月球绕地球的运动近似看做是匀速圆周运动。试求出月球绕地球运动的轨道半径
,且把月球绕地球的运动近似看做是匀速圆周运动。试求出月球绕地球运动的轨道半径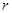 。
。
在某未知星球表面距地面6m的高度将一物体以水平速度15m/s抛出,落地时水平位移为30m
(1)求此星球表面的重力加速度
(2)若此星球的半径为5000km,求此星球的质量(保留一位有效数字)(G=6.67×10-11N·m2/kg2)
为了实现登月计划,先要测算地月之间的距离。已知地球表面重力加速度为g,地球半径为R,在地面附近物体受到地球的万有引力近似等于物体在地面上的重力,又知月球绕地球运动的周期为T,万有引力常量为G。则:
(1)地球的质量为多少?(2)地月之间的距离约为多少?
已知地球半径为R,地球表面重力加速度为g,不考虑地球自转的影响。
(1)推导第一宇宙速度v1的表达式;
(2)若卫星绕地球做匀速圆周运动,运行轨道距离地面高度为h,求卫星的运行周期T。
某中子星的质量大约与太阳的质量相等,为2×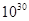 kg,但是它的半径才不过10km,求:(1)此中子星表面的自由落体加速度。
kg,但是它的半径才不过10km,求:(1)此中子星表面的自由落体加速度。
(2)贴近中子星表面,沿圆轨道运动的小卫星的速度。
(已知引力常量为G=6.67×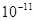 N
N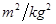


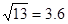 )
)
(12分)我国首个月球探测计划“嫦娥工程”将分三个阶段实施,大约用十年左右时间完成,这极大的提高了同学们对月球的关注程度。以下是某同学就有关月球的知识设计的两个问题,请你解答:
⑴若已知地球半径为R,地球表面的重力加速度为g,月球绕地球运动的周期为T,且把月球绕地球的运动近似看做是匀速圆周运动。试求出月球绕地球运动的轨道半径。
⑵若某位宇航员随登月飞船登陆月球后,在月球表面某处以速度v0竖直向上抛出一个小球,经过时间t,小球落回到抛出点。已知月球半径为R月,万有引力常量为G。试求出月球的质量M月。
为了探测某星球,载着登陆舱的探测飞船绕着该星球做匀速圆周运动,测得其周期为T1,轨道半径为r1;随后登陆舱脱离飞船,变轨到离星球表面很近的轨道上做匀速圆周运动,测得其周期为T2。已知万有引力常量为G。求:
(1)该星球的质量;
(2)星球表面的重力加速度。
一宇航员为了估测某一星球表面的重力加速度和该星球的质量,在该星球的表面做自由落体实验:让小球在离地面h高处自由下落,他测出经时间t小球落地,又已知该星球的半径为R,忽略一切阻力。求:
(1)该星球表面的重力加速度g;
(2)该星球的质量M;
(3)该星球的第一宇宙速度V.
我国已启动“登月工程”,设想在月球表面上,宇航员测出小物块自由下落h高度所用的时间为t。当飞船在靠近月球表面圆轨道上飞行时,测得其环绕周期是T,已知引力常量为G。根据上述各量,试求:
⑴月球表面的重力加速度;
⑵月球的质量。
宇航员站在一质量分布均匀星球表面上某高h处,沿水平方向抛出一个小球.测得落地时间为t.该星球的半径为R,万有引力常量为G,求
(1)该星球的质量M.
(2)该星球的密度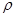
(3)该星球的第一宇宙速度
已知引力常量为G,地球的质量为M,地球的半径为R,某飞船绕地球做匀速圆周运动时距地面的高度为h.根据以上条件,试求该飞船绕地球做匀速圆周运动时的线速度大小?(用题中字母表示结果)