已知万有引力常量G,地球半径R1,地球和太阳之间的距离r1,地球绕太阳公转的周期T1,月球半径R2,地球和月亮之间的距离r2,月球绕地球公转的周期T2,地球表面的重力加速度g。请根据已知条件用二种估算方法地球的质量M。
两颗人造卫星A、B绕地球作匀速圆周运动,运动的周期之比为TA:TB=1:27,求:①、两卫星轨道半径之比;②、两卫星运动速率之比。
有一行星密度为地球密度的一半,表面重力加速度为地球的2倍,则该行星质量为地球的_________倍,若地球同步卫星的高度为地球半径的6倍,该行星的同步卫星的高度为其半径的2.5倍,则该行星的自转周期为__________小时。
关于地球同步卫星,下列说法中正确的是:
| A.地球同步卫星只是依靠惯性运动 |
| B.质量不同的地球同步卫星轨道高度相同 |
| C.质量不同的地球同步卫星周期不同 |
| D.所有地球同步卫星的加速度大小相同 |
若人造卫星绕地球做匀速圆周运动,则离地球越远的卫星:
| A.速度越小 | B.角速度越大 | C.加速度越大 | D.周期越长 |
一个行星,其半径是地球半径的2倍,质量是地球的8倍,则它表面的重力加速度是地球表面重力加速度的:
| A.16倍 | B.4倍 | C.2倍 | D.0.5倍 |
对于万有引力定律的表达式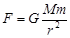 ,下面说法中正确的是:
,下面说法中正确的是:
| A.公式中的G为引力常量,它是开普勒用实验方法测定的 |
| B.当r趋近于零时,万有引力F趋向于无穷大 |
| C.m与M受到的引力总是大小相等的,而与m、M是否相等无关 |
| D.m与M受到的引力总是大小相等、方向相反,是一对平衡力 |
人造地球卫星在半径为r的轨道上绕地球作匀速圆周运动,卫星所受的向心力与轨道半径r的关系,下列说法中正确的是:
A.由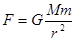 可知,向心力与r2成反比 可知,向心力与r2成反比 |
B.由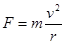 可知,向心力与r成反比 可知,向心力与r成反比 |
C.由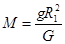 可知,向心力与r成正比 可知,向心力与r成正比 |
D.由 可知,向心力与r 无关 可知,向心力与r 无关 |
为了估算太阳的质量,需要知道绕太阳做匀速圆周运动的行星的( )
| A.运转周期和轨道半径 | B.质量和运转周期 |
| C.线速度和质量 | D.环绕速度和质量 |
宇宙飞船以a=g/2的加速度匀加速上升,由于超重现象,用弹簧秤测得质量为10kg的物体重量为75N,由此可求飞船所处位置距地面高度为多少?(地球半径R=6400km,g=10m/s2)
宇航员在月球上做竖直上抛运动的实验,将某物体由月球表面以初速度v0释放,到达最大高度为h,设月球半径为R.据上述信息,求飞船在月球表面附近绕月球做匀速圆周运动所必须具有的速率.
如图所示,发射地球同步卫星时,先将卫星发射至近地圆轨道1,然后经点火将卫星送入椭圆轨道2,然后再次点火,将卫星送入同步轨道3.轨道1、2相切于Q点,2、3相切于P点,则当卫星分别在1、2、3轨道上正常运行时,下列说法中正确的是( ).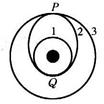
| A.卫星在轨道3上的速率大于在轨道1上的速率 |
| B.卫星在轨道3上的角速度大于在轨道1上的角速度 |
| C.卫星在轨道1上经过Q点时的加速度大于它在轨道2上经过Q点时的加速度 |
| D.卫星在轨道2上经过P点时的加速度等于它在轨道3上经过P点时的加速度 |
同步卫星离地球球心的距离为r,运行速率为v1,加速度大小为a1,地球赤道上的物体随地球自转的向心加速度大小为a2,第一宇宙速度为v2,地球半径为R。则( )
| A.a1:a2=" R:" r |
| B.a1:a2=R2:r2 |
| C.v1:v2=R2:r2 |
D.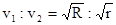 |