高中物理平抛运动计算题

如图所示，AB是半径为R的1/4光滑圆弧轨道，B点的切线沿水平方向， 且B点离水平地面的高度为h, 有一物体（可视为质点）从A点由静止开始滑下，到达B点后水平飞出。（设重力加速度为g）求：（1）物体运动到B点时的速度（2）物体落地点C到B点的水平距离

小明站在水平地面上，手握不可伸长的轻绳一端，绳的另一端系有质量为m的小球，甩动手腕，使球在竖直平面内做圆周运动。当球某次运动到最低点时，绳突然断掉，球飞行水平距离d后落地，如右图所示．已知握绳的手离地面高度为d，手与球之间的绳长为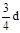，重力加速度为g。忽略手的运动半径和空气阻力。

(1)求绳断时球的速度大小v    
(2)问绳能承受的最大拉力多大？
(3)改变绳长，使球重复上述运动，若绳仍在球运动到最低点时断掉，且绳的最大承受力不变，要使球抛出的水平距离最大，绳长应为多少？最大水平距离为多少？

(18分)如图所示，粗糙斜直轨道PA和两个光滑圆弧轨道、组成的S形轨道，斜轨道与圆弧轨道在A点光滑连接，B点是最低点，已知,圆弧轨道半径均为R，两圆弧交接处C、D之间留有很小空隙，刚好能够使小球通过，CD之间距离可忽略。斜轨道最高点P与水平面BQ的高度差为h=6.5R。从P点静止释放一个质量为m可视为质点的小球，小球沿S形轨道运动后从G点水平飞出，落到水平地面上，落点Q点到B点的距离为x=4R。不计空气阻力，重力加速度为g，求：

（1）小球从G点水平飞出时的速度多大？
（2）小球运动到圆形轨道最低点B点时对轨道的压力；
（3）小球与轨道PA间的动摩擦因数μ。

(15分)如图所示，一质量为m、电荷量为q的带正电的小球以水平初速度v₀从离地高为h的地方做平抛运动，落地点为N，不计空气阻力，求：

(1)若在空间加一个竖直方向的匀强电场，使小球沿水平方向做匀速直线运动，则场强E为多大？
(2)若在空间再加上一个垂直于纸面向外的匀强磁场，小球的落地点仍为N，则磁感应强度B为多大？

如图所示，空间存在着方向竖直向上的匀强电场和方向垂直于纸面向内，磁感应强度大小为B的匀强磁场，带电量为+q、质量为m的小球Q静置在光滑绝缘的水平高台边缘，另一质量为m不带电的绝缘小球P以水平初速度v₀向Q运动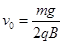，小球P、Q正碰过程中没有机械能损失且电荷量不发生转移，已知匀强电场的电场强度E=，水平台面距离地面高度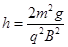，重力加速度为g，不计空气阻力。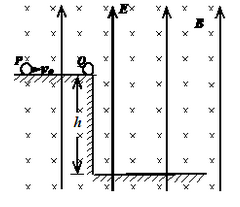

（1）求P、Q两球首次发生弹性碰撞后，小球Q的速度大小；
（2）P、Q两球首次发生弹性碰撞后，经多少时间小球P落地，落地点与平台边缘间的水平距离多大？
（3）若撤去匀强电场，并将小球Q重新放在平台边缘，小球P仍以水平初速度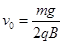向Q运动，小球Q的运动轨迹如图所示，已知Q球在最高点和最低点所受全力的大小相等，求小球Q在运动过程中的最大速度和第一次下降的最大距离H。

如图所示，半径R=0.80m的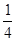光滑圆弧轨道竖直固定，过最低点的半径OC处于竖直位置，其右方有底面半径r=0.2m的转筒，转筒顶端与C等高，下部有一小孔，距顶端h=1m，转筒的轴线与圆弧轨道在同一竖直平面内，开始时小孔也在这一平面内的图示位置．现使一质量m=0.1kg的小物块自A点由静止开始下落后打在圆弧轨道上的B点但不反弹，在瞬间碰撞过程中，小物块沿半径方向的分速度立刻减为0，沿切线方向的分速度不变．此后，小物块沿圆弧轨道滑下，到达C点时触动光电装置，使转筒立刻以某一角速度匀速转动起来，且小物块最终正好进入小孔．已知A、B到圆心O的距离均为R，与水平方向的夹角均为θ=30°，不计空气阻力，g取l0m/s²，求：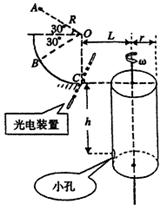

（1）小物块刚下落到B点时，在与B点碰撞前的瞬时速度的大小；
（2）小物块到达C点时受到轨道的支持力的大小；  
（3）转筒轴线距C点的距离L；
（4）转筒转动的角速度ω.

如图所示，小车A的顶部距地面高度为H=0.8m，小车质量m₁=2kg，它受地面阻力大小为其对地面压力大小的0.2倍，在其顶部右前方边缘处放有一个质量为m₂=8kg的物体B（大小忽略不计），物体B与小车A之间的最大静摩擦力为F_f=28N。在小车的左端施加一个水平向左，大小为F₀=6N的恒力作用，整个装置处于静止状态。现用一逐渐增大的水平力F作用在B上，使A、B共同向右运动，当F增大到某一值时，物体B刚好从小车前端脱离。重力加速度g="10" m/s².

求（1）物体B刚好从小车前端脱离时水平力F的大小。
（2）若物体B刚好从小车前端脱离时，小车A、物体B的共同速度大小为2m/s，此时立即撤去水平力F，计算当物体B落地时与小车A右前端的水平距离。

如图所示，小球从A点以固定的初速度v₀水平抛出，空气阻力不计，A点右下方有一带挡板的轮子，轮子与小球运动轨迹在同一竖直面内。轮子的半径为R，抛出点A比轮轴高h，挡板的初位置在与轮轴等高的B点，调整轮轴O的位置，使平抛轨迹与轮缘相切于C，OC与OB间夹角为θ角。求：

(l)小球抛出的初速度v₀大小为多少；
(2)小球抛出的瞬间轮子开始顺时针匀速转动，若不计挡板大小，要使小球打在挡板上，轮子转动的角速度为多少？

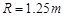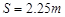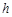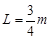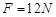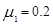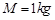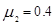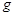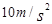如图所示，四分之一圆轨道OA与传送带相切相连，下方的CD水平轨道与他们在同一竖直面内。圆轨道OA的半径，传送带长，圆轨道OA光滑，AB与CD间的高度差为。一滑块从O点静止释放，当滑块经过B点时（无论传送带是否运动），静止在CD上的长为的木板（此时木板的末端在B点的正下方）在的水平恒力作用下启动，此时滑块落入木板中，已知滑块与传送带的摩擦因数，木板的质量，木板与CD间的摩擦因数为，取，求：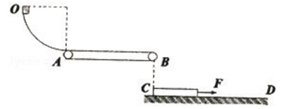

（1）如果传送带静止，求滑块到达B点的速度。
（2）如果传送带静止，求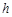的取值范围。
（3）如果传送带可以以任意速度传动，取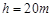，试判断滑块还能否落在木板上。

如图，在粗糙水平台阶上静止放置一质量m=0.5kg的小物块，它与水平台阶表面的动摩擦因数μ=0.5，且与台阶边缘O点的距离s=5m．在台阶右侧固定了一个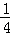圆弧挡板，圆弧半径R=1m，圆弧的圆心也在O点．今以O点为原点建立平面直角坐标系．现用F=5N的水平恒力拉动小物块，一段时间后撤去拉力，小物块最终水平抛出并击中挡板．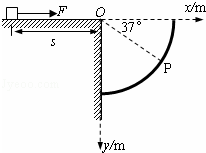

（1）若小物块恰能击中挡板上的P点（OP与水平方向夹角为37°），求其离开O点时的速度大小；
（2）为使小物块击中挡板，求拉力F作用的最短时间；
（3）改变拉力F的作用时间，使小物块击中挡板的不同位置，求击中挡板时小物块动能的最小值．

某人站在高60 m的平台边缘，以20 m/s的初速度竖直向上抛出一石块，不考虑空气阻力，取g="10" m/s²求：
（1）石块上升的最大高度。
（2）石块从抛出到落地的时间。
（3）石块落到地面时的速度。

如图所示，已知塔高H＝45m，在与塔底部水平距离为x处有一电子抛靶装置，圆形靶可被竖直向上抛出，初速度为υ₁，且大小可以调节．当该人看见靶被抛出时立即射击，子弹以υ₂＝100m/s的速度水平飞出．不计人的反应时间及子弹在枪膛中的运动时间，且忽略空气阻力及靶的大小（g取10 m/s²）。

（1）若x＝200m，υ₁＝20m/s时，试通过计算说明靶能否被击中？
（2）当x的取值在什么范围时，无论υ₁多大，靶都不能被击中？

某校物理兴趣小组决定举行遥控赛车比赛，比赛路径如图所示。可视为质点的赛车从起点A出发，沿水平直线轨道运动L后，由B点进入半径为R的光滑竖直半圆轨道，并通过半圆轨道的最高点C，才算完成比赛。B是半圆轨道的最低点，水平直线轨道和半圆轨道相切于B点。已知赛车质量m=0．5kg，通电后以额定功率P=2W工作，进入竖直圆轨道前受到的阻力恒为F_f=0．4N，随后在运动中受到的阻力均可不计，L=10．00m，R=0．32m，(g取10m/s²)。求：

（1）要使赛车完成比赛，赛车在半圆轨道的B点对轨道的压力至少多大；
（2）要使赛车完成比赛，电动机至少工作多长时间；
（3）若电动机工作时间为 t₀=5s，当R为多少时赛车既能完成比赛且飞出的水平距离又最大，水平距离最大是多少。

如图所示是某次四驱车比赛的轨道某一段。小明控制的四驱车（可视为质点），质量m=1.0kg，额定功率为P=7W。小明的四驱车到达水平平台上A点时速度很小（可视为0），此时启动四驱车的发动机并直接使发动机的功率达到额定功率，一段时间后关闭发动机。当四驱车由平台边缘点飞出后，恰能沿竖直光滑圆弧轨道CDE上C点的切线方向飞入圆形轨道。已知AB间的距离L=6m，BF间高度差h=0.8m，圆轨道的半径R=1m，∠COD=53°，四驱车在AB段运动时的阻力恒为1N。重力加速度g取10m/s²，不计空气阻力。sin53°=0.8，cos53°=0.6，求：

（1）求四驱车到达C点时的速度大小；
（2）发动机在水平平台上工作的时间；
（3）四驱车第一次经过D点时对轨道的压力大小。

(16分)在竖直平面内固定一轨道ABCO， AB段水平放置，长为4 m，BCO段弯曲且光滑，轨道在O点的曲率半径为1.5 m；一质量为1.0 kg、可视作质点的圆环套在轨道上，圆环与轨道AB段间的动摩擦因数为0.5。建立如图所示的直角坐标系，圆环在沿x轴正方向的恒力F作用下，从A（-7,2）点由静止开始运动，到达原点O时撤去恒力F，水平飞出后经过D（6，3）点。重力加速度g取10m/s²，不计空气阻力。求：
⑴圆环到达O点时对轨道的压力；
⑵恒力F的大小；
⑶圆环在AB段运动的时间。