如图所示，在水平地面上固定一个倾角θ=37O、表面光滑且很长的斜面体，物体A以vl=6m/s的初速度沿斜面上滑，同时在物体A的正上方，有一物体B以某一初速度水平抛出。如果当A上滑到最高点时恰好被B物体击中。若A、B均可看作质点，sin37O=0，6，cos370=0．8，g取10m/s2，
试求：
物体A上滑到最高点所用的时间t；
物体B 抛出时的初速度v2；
物体A、B间初始位置的高度差h。
如图，从地面上方某点，将一小球以10m/s的初速度沿水平方向抛出。小球经过ls落地。不计空气阻力，g=1Om/s2。则可求出
| A．小球抛出时离地面的高度是10m |
| B．小球从抛出点到落地点的位移大小是10m |
| C．小球落地时的速度大小是l5m/s |
| D．小球落地时的速度方向与水平地面成45O角 |
如图所示，AB为斜面，BC为水平面，从A点以水平初速度
向右抛出一小球，其落点与A的水平距离为
，若从A点以水平初速度
向右抛出同一小球，其落点与A的水平距离为
，不计空气阻力，则
的比值可能为
| A．1：2 | B．1：4 |
| C．1：10 | D．1：12 |
将小球从如图所示的阶梯状平台上以4 m/s的速度水平抛出，所有台阶的高度和宽度均为1.0 m，取g＝10 m/s2，小球抛出后首先落到的台阶是
| A．第一级台阶 | B．第二级台阶 |
| C．第三级台阶 | D．第四级台阶 |
在平坦的垒球运动场上，质量为m的垒球以速度v水平飞来，击球手挥动球棒将垒球等速水平反向击出，垒球飞行一段时间t 后落地。若不计空气阻力，则（ ）
| A．垒球落地时瞬时速度的大小仅由初速度决定 |
| B．垒球所受球棒的水平平均作用力为2mv/t |
| C．垒球在空中运动的水平位置仅由初速度决定 |
| D．垒球在空中运动的时间仅由击球点离地面的高度决定 |
平抛运动可以分解为水平和竖直两个方向的直线运动，在同一坐标系中作出这两个分运动的速率－时间图像，如图所示，假若平抛运动的时间大于2t1，则下列说法中正确的是
| A．图线2表示竖直分运动的速率－时间图线 |
| B．t1时刻的速度方向与初速度方向夹角为30° |
| C．t1时间内的竖直位移与水平位移之比为1：2 |
| D．2t1时刻的速度方向与初速度方向的夹角为60° |
如图所示，在斜面顶端a处以速度va水平抛出一小球，经过时间ta 恰好落在斜面底端P处；今在P点正上方与a等高的b处以速度vb水平抛出另一小球，经过时间tb恰好落在斜面的中点处．若不计空气阻力，下列关系式正确的是（ ）
| A．va＝vb | B．va＝vb | C．ta＝tb | D．ta＝2tb |
从某高度处以v0="15" m／s的初速度水平抛出一物体，经时间t=2s落地，g取10m／s2，求：
（1）物体抛出时的高度y和物体抛出点与落地点间的水平距离x；
（2）物体落地时的速度大小v。
平抛运动可以分解为水平和竖直两个方向的直线运动，在同一坐标系中作出这两个分运动的v-t图像，则：
| A．图线2表示竖直分运动的v–t图线 |
| B．这两个直线运动的合运动还是直线运动 |
| C．水平方向的速度总大于竖直方向的速度 |
| D．t1时刻水平方向的速度的与竖直方向的速度大小相等 |
如图所示，足够长的斜面与水平面之间的夹角为45°，在斜面底端A 点正上方高度为6m处的O点，以某速度水平抛出一个小球，小球飞行一段时间后恰能垂直撞在斜面上，则小球从抛出点到撞击点间的水平位移的大小为
| A．2m | B．4m | C．6m | D．9m |
如图所示，一固定斜面的倾角为α，高为h，一小球从斜面顶端沿水平方向落至斜面底端，不计小球运动中所受的空气阻力，设重力加速度为g，则小球从抛出到离斜面距离最大所经历的时间为
A． |
B． |
C． |
D． |
如图所示，在倾角为θ的斜面上以速度v0水平抛出一小球，设斜面足够长，则从抛出开始计时，经过时间t1= 时，小球落到斜面上；经过时间t2= 时，小球离斜面的距离达到最大。
从倾角为θ=30°的斜面M点以初动能E=6J向下坡方向平抛出一个小球，则小球落到斜面上N点时的动能E’为多少?( )
| A．8J | B．12J | C．l4J | D．18J |
如图所示，在水平地面上O点正上方的A、B两点分别水平抛出一小球，则关于两小球着地情况的描述正确的是( )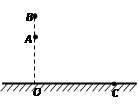 
A．两球可能都落在水平面上的C点
B．若两球都落在C点，落地速度方向可能相同
C．若两球都落在C点，落地速度大小可能相同
D．若两球都落在C点，落地速度的大小和方向可能都相同
粤公网安备 44130202000953号