高中物理牛顿运动定律的综合应用试题

如图，一竖直圆管质量为 $M$，下端距水平地面的高度为 $H$，顶端塞有一质量为 $m$的小球。圆管由静止自由下落，与地面发生多次弹性碰撞，且每次碰撞时间均极短；在运动过程中，管始终保持竖直。已知 $M=4m$，球和管之间的滑动摩擦力大小为 $4\mathit{mg}$， $g$为重力加速度的大小，不计空气阻力。

（1）求管第一次与地面碰撞后的瞬间，管和球各自的加速度大小；

（2）管第一次落地弹起后，在上升过程中球没有从管中滑出，求管上升的最大高度；

（3）管第二次落地弹起的上升过程中，球仍没有从管中滑出，求圆管长度应满足的条件。

如图，两个滑块 A和 B的质量分别为 $m_A=1\text{kg}$ 和 $m_B=5\text{kg}$ ，放在静止于水平地面上的木板的两端，两者与木板间的动摩擦因数均为 ${\mu }_1=0.5$ ；木板的质量为 $m=4\text{kg}$ ，与地面间的动摩擦因数为 ${\mu }_2=0.1$ 。某时刻 A、 B两滑块开始相向滑动，初速度大小均为 $v_0=3\text{m/s}$ 。 A、 B相遇时， A与木板恰好相对静止。设最大静摩擦力等于滑动摩擦力，取重力加速度大小 $g=10\text{m/}{\text{s}}^2$ 。求

（1） B与木板相对静止时，木板的速度；

（2） A、 B开始运动时，两者之间的距离。

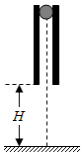
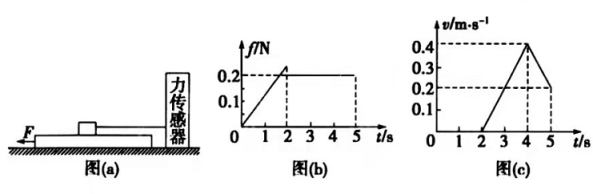
如图（a），物块和木板叠放在实验台上，物块用一不可伸长的细绳与固定在实验台上的力传感器相连，细绳水平。 $\mathrm{t}=0$ 时，木板开始受到水平外力F的作用，在 $\mathrm{t}=4s$ 时撤去外力。细绳对物块的拉力 $\mathrm{f}$ 随时间 $\mathrm{t}$ 变化的关系如图（b）所示，木板的速度 $\mathrm{v}$ 与时间 $\mathrm{t}$ 的关系如图（c）所示。木板与实验台之间的摩擦可以忽略。重力加速度取 $\mathrm{g}=10m/{\mathrm{s}}^2$ 。由题给数据可以得出（ ）

A．	木板的质量为 $1\mathrm{kg }$	B．	$\mathrm{ }2s~4s$ 内，力 $\mathrm{F}$ 的大小为 $0.4N$
C．	$0~2s$ 内，力 $\mathrm{F}$ 的大小保持不变	D．	物块与木板之间的动摩擦因数为 $0.2$

一细绳跨过悬挂的定滑轮，两端分别系有小球 $A$和 $B$，如图所示。一实验小组用此装置测量小球 $B$运动的加速度。令两小球静止，细绳拉紧，然后释放小球，测得小球 $B$释放时的高度 $h_0=0.590m$，下降一段距离后的高度 $h=0.100m$；由 $h_0$下降至 $h$所用的时间 $T=0.730s$。由此求得小球 $B$加速度的大小为 $a=$　　 $m/s^2$（保留3位有效数字）。从实验室提供的数据得知，小球 $A$、 $B$的质量分别为 $100.0g$和 $150.0g$，当地重力加速度大小为 $g=9.80m/s^2$．根据牛顿第二定律计算可得小球 $B$加速度的大小为 $a\text{'}=$　　 $m/s^2$（保留3位有效数字）。可以看出， $a\text{'}$与 $a$有明显差异，除实验中的偶然误差外，写出一条可能产生这一结果的原因：　　。

一质点做匀速直线运动，现对其施加一恒力，且原来作用在质点上的力不发生改变，则 （   ）

A．	质点速度的方向总是与该恒力的方向相同
B．	质点速度的方向不可能总是与该恒力的方向垂直.
C．	质点加速度的方向总是与该恒力的方向相同
D．	质点单位时间内速率的变化量总是不变

如图，一倾角为α的光滑固定斜面的顶端放有质量 $M＝0.06\mathit{kg}$ 的 $U$ 形导体框，导体框的电阻忽略不计；一电阻 $R＝3\Omega$ 的金属棒 $\mathit{CD}$ 的两端置于导体框上，与导体框构成矩形回路 $\mathit{CDEF}$ ； $\mathit{EF}$ 与斜面底边平行，长度 $L＝0.6m$ 。初始时 $\mathit{CD}$ 与 $\mathit{EF}$ 相距 $s_0＝0.4m$ ，金属棒与导体框同时由静止开始下滑，金属棒下滑距离 $s_1＝\frac{3}{16}m$ 后进入一方向垂直于斜面的匀强磁场区域，磁场边界（图中虚线）与斜面底边平行；金属棒在磁场中做匀速运动，直至离开磁场区域。当金属棒离开磁场的瞬间，导体框的 $\mathit{EF}$ 边正好进入磁场，并在匀速运动一段距离后开始加速。已知金属棒与导体框之间始终接触良好，磁场的磁感应强度大小 $B＝1T$ ，重力加速度大小取 $g＝10m/s^2$ ， $\mathit{sin\alpha }＝0.6$ 。求

（1）金属棒在磁场中运动时所受安培力的大小；

（2）金属棒的质量以及金属棒与导体框之间的动摩擦因数；

（3）导体框匀速运动的距离。

一篮球质量为 $m＝0.60\mathit{kg}$，一运动员使其从距地面高度为 $h_1＝1.8m$处由静止自由落下，反弹高度为 $h_2＝1.2m$。若使篮球从距地面 $h_3＝1.5m$的高度由静止下落，并在开始下落的同时向下拍球，球落地后反弹的高度也为 $1.5m$。假设运动员拍球时对球的作用力为恒力，作用时间为 $t＝0.20s$；该篮球每次与地面碰撞前后的动能的比值不变。重力加速度大小取 $g＝10m/s^2$，不计空气阻力。求：

（1）运动员拍球过程中对篮球所做的功；

（2）运动员拍球时对篮球的作用力的大小。

水平地面上有一质量为 $m_1$ 的长木板，木板的左端上有一质量为 $m_2$ 的物块，如图（a）所示。用水平向右的拉力F作用在物块上，F随时间t的变化关系如图（b）所示，其中 $F_1$ 、 $F_2$ 分别为 $t_1$ 、 $t_2$ 时刻F的大小。木板的加速度 $a_1$ 随时间t的变化关系如图 $（c）$ 所示。已知木板与地面间的动摩擦因数为 ${\mu }_1$ ，物块与木板间的动摩擦因数为μ ₂。假设最大静摩擦力均与相应的滑动摩擦力相等，重力加速度大小为g。则（　　）

A．	$F_1＝{\mu }_1{m}_{1}g$
B．	$F_2=\frac{m_2(m_1+m_2)}{m_1}（{\mu }_2﹣{\mu }_1）g$
C．	${\mu }_2＞\frac{m_1+m_2}{m_2}{\mu }_1$
D．	在 $0～t_2$ 时间段物块与木板加速度相等

一质量为 m的物体自倾角为 α的固定斜面底端沿斜面向上滑动。该物体开始滑动时的动能为 E _k，向上滑动一段距离后速度减小为零；此后物体向下滑动，到达斜面底端时动能为 $\frac{E_k}{5}$ 。已知sin α＝0.6，重力加速度大小为g。则（   ）

A．	物体向上滑动的距离为 $\frac{E_k}{2\mathit{mg}}$
B．	物体向下滑动时的加速度大小为 $\frac{g}{5}$
C．	物体与斜面间的动摩擦因数等于0.5
D．	物体向上滑动所用的时间比向下滑动的时间长

如图，将光滑长平板的下端置于铁架台水平底座上的挡板 P处，上部架在横杆上。横杆的位置可在竖直杆上调节，使得平板与底座之间的夹角 θ可变。将小物块由平板与竖直杆交点 Q处静止释放，物块沿平板从 Q点滑至 P点所用的时间 t与夹角 θ的大小有关。若 θ由30°逐渐增大至60°，物块的下滑时间 t将（   ）

A．

逐渐增大

B．

逐渐减小

C．

先增大后减小

D．

先减小后增大

单板滑雪 $U$型池比赛是冬奥会比赛项目，其场地可以简化为如图甲所示的模型： $U$形滑道由两个半径相同的四分之一圆柱面轨道和一个中央的平面直轨道连接而成，轨道倾角为 $17.2°$。某次练习过程中，运动员以 $v_M=10m/s$的速度从轨道边缘上的 $M$点沿轨道的竖直切面 $\mathit{ABCD}$滑出轨道，速度方向与轨道边缘线 $\mathit{AD}$的夹角 $\alpha =72.8°$，腾空后沿轨道边缘的 $N$点进入轨道。图乙为腾空过程左视图。该运动员可视为质点，不计空气阻力，取重力加速度的大小 $g=10m/s^2$， $\sin 72.8°=0.96$， $\cos 72.8°=0.30$。求：

（1）运动员腾空过程中离开 $\mathit{AD}$的距离的最大值 $d$；

（2） $M$、 $N$之间的距离 $L$。

如图，相距 $L=11.5m$的两平台位于同一水平面内，二者之间用传送带相接。传送带向右匀速运动，其速度的大小 $v$可以由驱动系统根据需要设定。质量 $m=10\mathit{kg}$的载物箱（可视为质点），以初速度 $v_0=5.0m/s$自左侧平台滑上传送带。载物箱与传送带间的动摩擦因数 $\mu =0.10$，重力加速度取 $g=10m/s^2$。

（1）若 $v=4.0m/s$，求载物箱通过传送带所需的时间；

（2）求载物箱到达右侧平台时所能达到的最大速度和最小速度；

（3）若 $v=6.0m/s$，载物箱滑上传送带△ $t=\frac{13}{12}s$后，传送带速度突然变为零。求载物箱从左侧平台向右侧平台运动的过程中，传送带对它的冲量。

如图， $U$ 形光滑金属框 $\mathit{abcd}$ 置于水平绝缘平台上， $\mathit{ab}$ 和 $\mathit{dc}$ 边平行，和 $\mathit{bc}$ 边垂直。 $\mathit{ab}$ 、 $\mathit{dc}$ 足够长，整个金属框电阻可忽略。一根具有一定电阻的导体棒 $\mathit{MN}$ 置于金属框上，用水平恒力 $F$ 向右拉动金属框，运动过程中，装置始终处于竖直向下的匀强磁场中， $\mathit{MN}$ 与金属框保持良好接触，且与 $\mathit{bc}$ 边保持平行。经过一段时间后 $($ 　　 $)$

A．	金属框的速度大小趋于恒定值
B．	金属框的加速度大小趋于恒定值
C．	导体棒所受安培力的大小趋于恒定值
D．	导体棒到金属框 $\mathit{bc}$ 边的距离趋于恒定值