高中物理试题

如图所示，绝缘轻杆的两端固定带有等量异号电荷的小球（不计重力）。开始时，两小球分别静止在 $A$ 、 $B$ 位置。现外加一匀强电场 $E$ ，在静电力作用下，小球绕轻杆中点 $O$ 转到水平位置。取 $O$ 点的电势为0．下列说法正确的有 $($ 　　 $)$

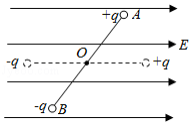
A．	电场 $E$ 中 $A$ 点电势低于 $B$ 点
B．	转动中两小球的电势能始终相等
C．	该过程静电力对两小球均做负功
D．	该过程两小球的总电势能增加

如图所示，小球 $A$ 、 $B$ 分别从 $2l$ 和 $l$ 的高度水平抛出后落地，上述过程中 $A$ 、 $B$ 的水平位移分别为 $l$ 和 $2l$ 。忽略空气阻力，则 $($ 　　 $)$

A．	$A$ 和 $B$ 的位移大小相等	B．	$A$ 的运动时间是 $B$ 的2倍
C．	$A$ 的初速度是 $B$ 的 $\frac{1}{2}$	D．	$A$ 的末速度比 $B$ 的大

甲、乙两颗人造卫星质量相等，均绕地球做圆周运动，甲的轨道半径是乙的2倍。下列应用公式进行的推论正确的有 $($ 　　 $)$

A．	由 $v=\sqrt{\mathit{gR}}$ 可知，甲的速度是乙的 $\sqrt{2}$ 倍
B．	由 $a={\omega }^{2}r$ 可知，甲的向心加速度是乙的2倍
C．	由 $F=G\frac{\mathit{Mm}}{r^2}$ 可知，甲的向心力是乙的 $\frac{1}{4}$
D．	由 $\frac{r^3}{T^2}=k$ 可知，甲的周期是乙的 $2\sqrt{2}$ 倍

某汽车的电源与启动电机、车灯连接的简化电路如图所示。当汽车启动时，开关 $S$ 闭合，电机工作，车灯突然变暗，此时 $($ 　　 $)$

A．	车灯的电流变小	B．	路端电压变小
C．	电路的总电流变小	D．	电源的总功率变大

中欧班列在欧亚大陆开辟了"生命之路"，为国际抗疫贡献了中国力量。某运送防疫物资的班列由40节质量相等的车厢组成，在车头牵引下，列车沿平直轨道匀加速行驶时，第2节对第3节车厢的牵引力为 $F$ ．若每节车厢所受摩擦力、空气阻力均相等，则倒数第3节对倒数第2节车厢的牵引力为 $($ 　　 $)$

A．

$F$

B．

$\frac{19F}{20}$

C．

$\frac{F}{19}$

D．

$\frac{F}{20}$

如图所示，一小物块由静止开始沿斜面向下滑动，最后停在水平地面上。斜面和地面平滑连接，且物块与斜面、物块与地面间的动摩擦因数均为常数。该过程中，物块的动能 $E_k$ 与水平位移 $x$ 关系的图象是 $($ 　　 $)$

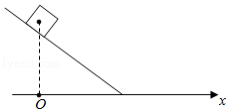
A．		B．
C．		D．

如图所示，两匀强磁场的磁感应强度 $B_1$ 和 $B_2$ 大小相等、方向相反。金属圆环的直径与两磁场的边界重合。下列变化会在环中产生顺时针方向感应电流的是 $($ 　　 $)$

A．	同时增大 $B_1$ 减小 $B_2$
B．	同时减小 $B_1$ 增大 $B_2$
C．	同时以相同的变化率增大 $B_1$ 和 $B_2$
D．	同时以相同的变化率减小 $B_1$ 和 $B_2$

电流互感器是一种测量电路中电流的变压器，工作原理如图所示。其原线圈匝数较少，串联在电路中，副线圈匝数较多，两端接在电流表上。则电流互感器 $($ 　　 $)$

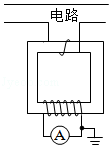
A．	是一种降压变压器
B．	能测量直流电路的电流
C．	原、副线圈电流的频率不同
D．	副线圈的电流小于原线圈的电流

质量为 $1.5\times {10}^3\mathit{kg}$ 的汽车在水平路面上匀速行驶，速度为 $20m/s$ ，受到的阻力大小为 $1.8\times {10}^{3}N$ ．此时，汽车发动机输出的实际功率是 $($ 　　 $)$

A．

$90W$

B．

$30\mathit{kW}$

C．

$36\mathit{kW}$

D．

$300\mathit{kW}$

如图所示，长为L、内壁光滑的直管与水平地面成30°角固定放置．将一质量为m的小球固定在管底，用一轻质光滑细线将小球与质量为M=km的小物块相连，小物块悬挂于管口．现将小球释放，一段时间后，小物块落地静止不动，小球继续向上运动，通过管口的转向装置后做平抛运动，小球在转向过程中速率不变．（重力加速度为g）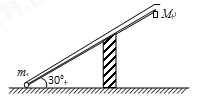

（1）求小物块下落过程中的加速度大小；
（2）求小球从管口抛出时的速度大小；
（3）试证明小球平抛运动的水平位移总小于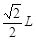

某地“欢乐谷”大型的游乐性主题公园，园内有一种大型游戏机叫“跳楼机”．让人体验短暂的“完全失重”，非常刺激．参加游戏的游客被安全带固定在座椅上，由电动机将座椅沿光滑的竖直轨道提升到离地面50m高处，然后由静止释放．为研究方便，认为人与座椅沿轨道做自由落体运动2s后，开始受到恒定阻力而立即做匀减速运动，且下落到离地面5m高处时速度刚好减小到零．然后再让座椅以相当缓慢的速度稳稳下落，将游客送回地面．（取g=10m/s²）

求：（1）座椅在自由下落结束时刻的速度是多大？
（2）在匀减速阶段，座椅对游客的作用力大小是游客体重的多少倍？

某同学在用如图所示的装置做“探究加速度与物体受力的关系”实验时，该同学在实验室找到了一个小正方体木块，接着用这个小正方体木块把小车轨道的一端垫高，通过速度传感器发现小车刚好做匀速直线运动。

（1）设小车的质量为M，正方体木块的边长为a，并用刻度尺量出图中AB的距离为l（a＜＜l且已知θ很小时tanθ≈sinθ），则小车向下滑动时受到的摩擦力为____________；
（2）然后用细线通过定滑轮挂上重物让小车匀加速下滑，不断改变重物的质量m，测出对应的加速度a，则下列图象中能正确反映小车加速度a与所挂重物质量m的关系的是____________。

测量木块与木板间动摩擦因数μ，某小组设计了使用位移传感器的图示实验装置，让木块从倾斜木板上一点A静止释放，位移传感器连接计算机描绘了滑块相对传感器的位移随时间变化规律如图

（1）根据下述图线计算t₀时刻速度大小v₁=      ，2t₀时刻速度大小v₂=      ,木块加速度a=      （用图中给出x₀、x₁、x₂、x₃、t₀表示）；
（2）已知重力加速度为g，测得木板的倾角为θ，木块的加速度为a ，则木块与长木板间动摩擦因数μ=             。

如图所示，A、B两物块的质量分别为2m和m，静止叠放在水平地面上．A、B间的动摩擦因数为μ，B与地面间的动摩擦因数为μ．最大静摩擦力等于滑动摩擦力，重力加速度为g．现对A施加一水平拉力F，则（   ）

A．当F＜2μmg 时，A、B都相对地面静止
B．当F＝μmg时，A的加速度为μg
C．当F＞3μmg时，A相对B滑动
D．无论F为何值，B的加速度不会超过μg

如图所示，A、B两球分别套在两光滑无限长的水平直杆上，两球通过一轻绳绕过一定滑轮（轴心固定不动）相连，某时刻连接两球的轻绳与水平方向的夹角分别为α、β，A球向左的速度为v，下列说法正确的是

A．此时B球的速度为
B．此时B球的速度为
C．当β增大到等于90°时，B球的速度达到最大，A球的速度为0
D．在整个运动过程中，绳对B球的拉力一直做正功