一汽车在平直公路上以20kW的功率行驶,t1时刻驶入另一段阻力恒定的平直公路,其v~t图象如图所示,已知汽车的质量为2×103kg。下列说法正确的是( )

| A.t1前汽车受到的阻力大小为1×103N |
| B.t1后汽车受到的阻力大小为4×103N |
| C.t1时刻汽车加速度大小突然变为1m/s2 |
| D.t1~t2时间内汽车的平均速度为7.5m/s |
如图所示,甲、乙两水平圆盘紧靠在一块,甲圆盘为主动轮,乙靠摩擦随甲无打滑转动.甲圆盘与乙圆盘的半径之比为r甲∶r乙=2∶1,两圆盘和小物体m1、m2之间的动摩擦因数相同,m1距O点为2r,m2距O′点为r,当甲缓慢转动起来且转速慢慢增加时( ).

| A.与圆盘相对滑动前m1与m2的角速度之比ω1∶ω2=2∶1 |
| B.与圆盘相对滑动前m1与m2的向心加速度之比a1∶a2=1∶2 |
| C.随转速慢慢增加,m1先开始滑动 |
| D.随转速慢慢增加,m2先开始滑动 |
如图所示,质量为M“的光滑斜面倾角为300,质量分别为M、m的两个物体通过细绳及轻弹簧连接于光滑轻滑轮两侧,斜面底端有一与斜面垂直的挡板.开始时用手按住物体M,此时M距离挡板的距离为s,滑轮两边的细绳恰好伸直,且弹簧处于原长状态.已知M=2m,空气阻力不计.松开手后,斜面体始终保持静止,则在M下滑过程中下列说法中正确的是( )
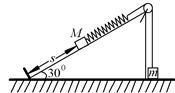
| A.M和m组成的系统机械能守恒 |
| B.当M的速度最大时(未碰到板),m与地面间的作用力不为零 |
| C.当M的速度最大时(未碰到板),水平面对斜面的支持力为(M’’+M+m)g |
| D.当m离开地面后M做匀速运动 |
如图甲所示,四个质量、形状相同的斜面体放在粗糙的水平面上,将四个质量相同的物块放在斜面顶端,因物块与斜面的摩擦力不同,四个物块运动情况不同.A物块放上后匀加速下滑,B物块获一初速度后匀速下滑,C物块获一初速度后匀减速下滑,D物块放上后静止在斜面上.若在上述四种情况下斜面体均保持静止且对地面的压力依次为F1、F2、F3、F4,则它们的大小关系是( )
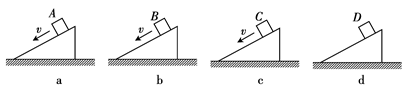
| A.F1<F2=F4<F3 | B.F1>F2>F3>F4 |
| C.F1=F2=F3=F4 | D.F1=F3<F2<F4 |
如图所示,质量分别为3m和m的两个可视为质点的小球a、b,中间用一细线连接,并通过另一细线将小球a与天花板上的O点相连,为使小球a和小球b均处于静止状态,且Oa细线向右偏离竖直方向的夹角恒为37°,需要对小球b朝某一方向施加一拉力F。若已知sin37°=0.6,cos37°=0.8,重力加速度为g,则当F的大小达到最小时,Oa细线对小球a的拉力大小为( )
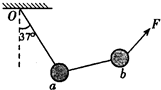
| A.4mg | B.3.2mg |
| C.2.4mg | D.3 mg |
物体以速度v匀速通过直线上的A、B两点,所用时间为t.现在物体从A点由静止出发,先做匀加速直线运动(加速度为a1)到某一最大速度vm,然后立即做匀减速直线运动(加速度大小为a2)至B点速度恰好减为0,所用时间仍为t,则物体的( )
A.vm可为许多值,与al、a2的大小有关
B.vm可为许多值,与al、a2的大小无关
C.al、a2必须满足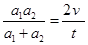
D.al、a2必须是一定的
如图所示,长为L的轻杆一端固定质量为m的小球,另一端固定在转轴O,现使小球在竖直平面内做圆周运动,P为圆周的最高点,若小球通过圆周最低点时的速度大小为 ,忽略摩擦阻力和空气阻力,则以下判断正确的是( ).
,忽略摩擦阻力和空气阻力,则以下判断正确的是( ).

| A.小球不能到达P点 |
B.小球到达P点时的速度大于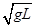 |
| C.小球能到达P点,且在P点受到轻杆向上的弹力 |
| D.小球能到达P点,且在P点受到轻杆向下的弹力 |
某战士在倾角为30o山坡上进行投掷手榴弹训练。他从A点以某一初速度v0沿水平方向投出手榴弹,正好落在B点,测得AB=90m。若空气阻力不计,(g=10m/s2)求: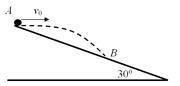
(1)手榴弹抛出的速度?
(2)从抛出开始经多长时间手榴弹与山坡间的距离最大?并求出此时手榴弹与山坡间的距离?
如图所示,质量为m的物体放在倾角为θ的粗糙斜面上,斜面固定在电梯中,物体和斜面保持相对静止。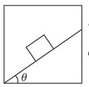
(1)若电梯匀速上升,求物块受到斜面的摩擦力和支持力是多少?
(2)若电梯以加速度a加速上升,求物块对斜面的摩擦力和压力是多少?
质量为2 kg的物体在水平推力F的作用下沿水平面做直线运动,一段时间后撤去F,其运动的v-t图象如图所示.g取10 m/s2,求:
(1)物体与水平面间的动摩擦因数μ;
(2)水平推力F的大小;
(3)0~10 s内物体运动位移的大小.
足够长的倾角θ=53°的斜面固定在水平地面上,一物体以v0=6.4 m/s的初速度从斜面底端向上滑行,该物体与斜面间的动摩擦因数μ=0.8,如图所示.(sin53°=0.8,cos53°=0.6,g取10 m/s2)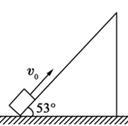
(1)求物体从开始到再次返回斜面底端所需的时间?
(2)求返回斜面底端时的速度?
(1)利用下图所示的装置研究小车加速度a和小车质量M的关系时,由于没有始终满足M>>m(m为砝码盘及砝码的总质量)的条件,结果得到的图像应是如下图中的图( )


(2)某同学设计了如下实验方案:

A.实验装置如图甲所示,一端系在滑块上的轻质细绳通过转轴光滑的轻质滑轮,另一端挂一重力为3.3N的钩码,用垫块将长木板的有定滑轮的一端垫起.调整长木板的倾角,直至轻推滑块后,滑块沿长木板向下做匀速直线运动;
B.保持长木板的倾角不变,取下细绳和钩码,接好纸带,接通打点计时器的电源,然后让滑块沿长木板滑下,打点计时器打下的纸带如图乙所示.
请回答下列问题:
①图乙中纸带的哪端与滑块相连?________(选填“左端”或“右端”).
②图乙中相邻两个计数点之间还有4个打点未画出,打点计时器接频率为50 Hz的交流电源,根据图乙求出滑块的加速度a=________m/s2.
③不计纸带与打点计时器间的阻力,滑块的质量M=________kg.(g取10 m/s2)
有同学利用如图所示的装置来验证力的平行四边形定则:在竖直木板上铺有白纸,固定两个光滑的滑轮A和B,将绳子打一个结点O,每个钩码的重量相等,当系统达到平衡时,根据钩码个数读出三根绳子的拉力TOA.TOB和TOC,回答下列问题:

(1)改变钩码个数,实验能完成的是
A.钩码的个数N1=N2=2,N3=4
B.钩码的个数N1=N3=3,N2=4
C.钩码的个数N1=N2=N3=4
D.钩码的个数N1=3,N2=4,N3=5
(2)在拆下钩码和绳子前,最必要的一个步骤是 .
A.标记结点O的位置,并记录OA.OB.OC三段绳子的方向
B.量出OA.OB.OC三段绳子的长度
C.用量角器量出三段绳子之间的夹角
D.用天平测出钩码的质量.
为了节省能量,某商场安装了智能化的电动扶梯。无人乘行时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速运转。一顾客乘扶梯上楼,恰好经历了这两个过程,如图所示。那么下列说法中正确的是( )
| A.顾客受到的支持力始终处大于重力 |
| B.顾客始先受到三个力的作用,然后受到两个力的作用 |
| C.顾客对扶梯作用的方向先指向右下方,再竖直向下 |
| D.顾客对扶梯作用力的方向先指向左下方,再竖直向下 |