对椭圆有结论一:椭圆 的右焦点为
的右焦点为 ,过点
,过点 的直线
的直线 交椭圆于
交椭圆于 两点,点
两点,点 关于
关于 轴的对称点为
轴的对称点为 ,则直线
,则直线 过点
过点 。类比该结论,对双曲线有结论二,根据结论二知道:双曲线
。类比该结论,对双曲线有结论二,根据结论二知道:双曲线 的右焦点为
的右焦点为 ,过点
,过点 的直线与双曲线
的直线与双曲线 右支有两交点
右支有两交点 ,若点
,若点 的坐标是
的坐标是 ,则在直线
,则在直线 与双曲线的另一个交点坐标是__________.
与双曲线的另一个交点坐标是__________.
某射击运动员在练习射击中,每次射击命中目标的概率是 ,则这名运动员在10次射击中,
,则这名运动员在10次射击中,
至少有9次命中的概率是 .(记 ,结果用含
,结果用含 的代数式表示)
的代数式表示)
(本小题满分13分)如图,在 中,
中, ,
,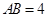 ,
, ,点
,点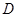 在线段
在线段 上,且
上,且 .
.
(Ⅰ)求 的长;
的长;
(Ⅱ)求 的值.
的值.
已知双曲线C: 的一个焦点是抛物线
的一个焦点是抛物线 的焦点,且双曲线 C的离心率为
的焦点,且双曲线 C的离心率为 ,那么双曲线C的方程为____;渐近线方程是____.
,那么双曲线C的方程为____;渐近线方程是____.
某种产品的加工需要A,B,C,D,E五道工艺,其中A必须在D的前面完成(不一定相邻),其它工艺的顺序可以改变,但不能同时进行,为了节省加工时间,B与C必须相邻,那么完成加工该产品的不同工艺的排列顺序有____种.(用数字作答)
已知双曲线C: 的一个焦点是抛物线
的一个焦点是抛物线 的焦点,且双曲线
的焦点,且双曲线
C的离心率为 ,那么双曲线C的方程为____.
,那么双曲线C的方程为____.
(本小题满分14分)如图,在三棱柱 中,各个侧面均是边长为
中,各个侧面均是边长为 的正方形,
的正方形, 为线段
为线段 的中点.
的中点.
(Ⅰ)求证: ⊥平面
⊥平面 ;
;
(Ⅱ)求证:直线 ∥平面
∥平面 ;
;
(Ⅲ)设 为线段
为线段 上任意一点,在
上任意一点,在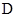
 内的平面区域(包括边界)是否存在点
内的平面区域(包括边界)是否存在点 ,使
,使
 ,并说明理由.
,并说明理由.