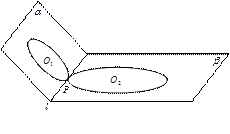
如图2,在 的二面角
的二面角 内,半径为1的圆
内,半径为1的圆
与半径为2的圆 分别在半平面
分别在半平面 、
、 内,且与棱
内,且与棱 切于
切于
同一点 ,则以圆
,则以圆 与圆
与圆 为截面的球的表面积为( )
为截面的球的表面积为( )
A. |
B.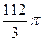 |
C.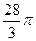 |
D. |
设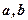 是两条不同的直线,
是两条不同的直线,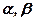 是两个不同的平面,则下列四个命题:
是两个不同的平面,则下列四个命题:
(1)若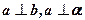 ,则
,则 ∥
∥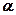 ;(2)若
;(2)若 ∥
∥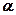 ,
, ,则
,则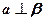
(3)若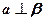 ,
, ,则
,则 ∥
∥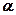 ;(4)若
;(4)若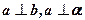 ,
, ,则
,则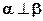
其中正确命题个数是( )个。
| A.0 | B.1 | C.2 | D.3 |
(甲)在平行六面体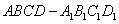 中,
中,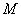 为
为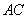 与
与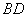 的交点,若
的交点,若 ,
,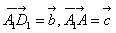 ,则下列向量与
,则下列向量与 相等的向量是( )
相等的向量是( )
A、 B、
B、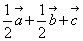 C、
C、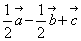 D、
D、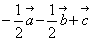
(乙)袋中有大小相同的4个红球,6个白球,每次从袋中摸取一球,每个球被取到的可能性相同,则不放回地取3个,至少有两个红球的概率为( )
A、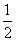 B、
B、 C、
C、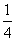 D、
D、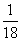
两个相同的等腰直角三角板,让其一直角边重合,且这两个直角三角板所在平面互相垂直,则这两个三角板斜边所在直线( )
| A.垂直 | B.成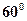 角 角 |
C.可能平行 | D.成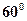 角或 角或 角 角 |
设有如下三个命题:甲:相交的直线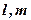 都在平面
都在平面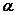 内,并且都不在平面
内,并且都不在平面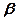 内;乙:直线
内;乙:直线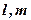 中至少有一条与平面
中至少有一条与平面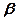 相交;丙:平面
相交;丙:平面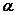 与平面
与平面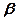 相交,当甲成立时( )
相交,当甲成立时( )
| A.乙是丙的充分不必要条件 | B.乙是丙的必要不充分条件 |
| C.乙是丙的充分必要条件 | D.乙既不是丙的充分条件也不是丙的必要条件 |
某大街在甲、乙、丙三处设有红绿灯,汽车在这三处因绿灯而通行的概率分别为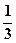 ,
,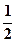 ,
, ,则汽车在这三处因遇红灯而停车一次的概率为( )
,则汽车在这三处因遇红灯而停车一次的概率为( )
A.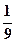 |
B. |
C.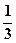 |
D. |
棱锥被平行于底面的平面所截,当截面分别平分侧棱,侧面积时所得截面相应面积分别为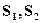 ,则
,则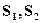 的大小关系为( )
的大小关系为( )
A. |
B.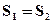 |
C. |
D.无法判断 |
、将一个四棱锥的每个顶点染上一种颜色,并使同一条棱的两端异色,若只有五种颜色可供使用,则不同的染色方法总数为( )种
| A.240 | B.300 | C.360 | D.420 |
一内侧边长为 的正方体容器被水充满,首先把半径为
的正方体容器被水充满,首先把半径为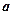 的球放入其中,再放入一个能被水完全淹没的小球,若想使溢出的水量最大,这个小球的半径为( )
的球放入其中,再放入一个能被水完全淹没的小球,若想使溢出的水量最大,这个小球的半径为( )
A.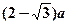 |
B. |
C. |
D.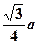 |