河南省郑州市盛同学校高二下学期期末数学试题(理科)
(本小题满分12分)甲、乙两人进行一种游戏,两人同时随机地喊出杠、虎、鸡、虫,按照
杠打虎、虎吃鸡、鸡吃虫、虫啃杠的原则决定胜负。 (比如甲喊杠的同时,乙若喊虎则乙输,乙若
喊虫则乙赢,乙若喊杠或鸡则不分胜负。) 若两人同时喊出一次后不分胜负则继续喊下去,直到
分出胜负。
(Ⅰ)喊一次甲就获胜的概率是多少?
(Ⅱ)甲在喊不超过三次的情况下就获胜的概率是多少?
(本小题满分12分)如图,已知四棱锥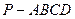 ,底面
,底面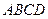 为菱形,
为菱形, ⊥平面
⊥平面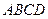 ,
, ,
, 、
、 分别是
分别是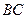 、
、 的中点。
的中点。
(Ⅰ)证明: ⊥
⊥ ;
;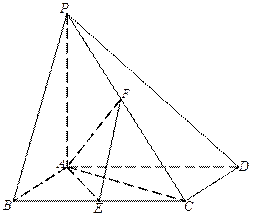 (Ⅱ)若
(Ⅱ)若 为
为 上的动点,
上的动点,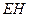 与平面
与平面 所成最大角的正切值为
所成最大角的正切值为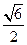 ,求二面角
,求二面角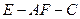 的余弦值。
的余弦值。
 、
、 与直线
与直线 都成异面直线,则
都成异面直线,则 ,则
,则 等于( )
等于( )

 ,则
,则 的值为( )
的值为( )




 ⊥平面
⊥平面 ,直线
,直线
 平面
平面 ,给出下列四个命题:
,给出下列四个命题: ②
② ③
③ ④
④
 的展开式中含有非零常数项,则正整数
的展开式中含有非零常数项,则正整数 的最小值为( )
的最小值为( )



 是函数
是函数 的导函数,
的导函数, 的图象如图1所示,
的图象如图1所示, 的图象最有可能的是( )
的图象最有可能的是( )

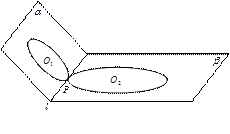
 的二面角
的二面角 内,半径为1的圆
内,半径为1的圆
 分别在半平面
分别在半平面 、
、 内,且与棱
内,且与棱 切于
切于 ,则以圆
,则以圆
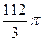
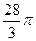

 的展开式中含
的展开式中含 项的系数为 。
项的系数为 。  和
和 都不发生的概率为
都不发生的概率为 ,
, 为 。
为 。 中,
中,  ,
, ,则
,则 与平面
与平面

 ,
, 有大于零的极值点,则
有大于零的极值点,则 的取值范围是 。
的取值范围是 。 的所有棱长都为2,
的所有棱长都为2, 为
为 的中点。
的中点。 ∥平面
∥平面 ;
; 所成的角。
所成的角。 
 的展开式中,名项系数的和与其各项二项式系数的和之比为32
的展开式中,名项系数的和与其各项二项式系数的和之比为32

 处取得极值,并且它的图象
处取得极值,并且它的图象 在点(1,0)处相切。
在点(1,0)处相切。 、
、 、
、 的值;
的值; 的单调区间。
的单调区间。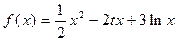 ,
,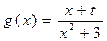 ,函数
,函数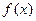
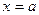 、
、 处取得极值,其中
处取得极值,其中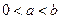 。
。 的取值范围;
的取值范围;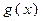 在
在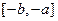 上的单调性;
上的单调性; ,若方程
,若方程 有3个不同的解,
有3个不同的解,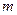 的取值范围。
的取值范围。 粤公网安备 44130202000953号
粤公网安备 44130202000953号