已知曲线y=x4+ax2+1在点(-1,a+2)处切线的斜率为8,则a=________.
若直线y= x+b是曲线y=lnx(x>0)的一条切线,则实数b=________.
x+b是曲线y=lnx(x>0)的一条切线,则实数b=________.
已知函数f(x)=1+ ,则f(x)在区间[1,2],
,则f(x)在区间[1,2], 上的平均变化率分别为________.
上的平均变化率分别为________.
若曲线f(x)=ax3+ln x存在垂直于y轴的切线,则实数a的取值范围是
________.
过点P(-1,2)且与曲线y=3x2-4x+2在点M(1,1)处的切线平行的直线
方程是________.
在区间[-6,6]内任取一个元素x0,抛物线x2=4y在x=x0处的切线的倾斜角为α,则α∈ 的概率为 .
的概率为 .
若曲线y=xα+1(α∈R)在点(1,2)处的切线经过坐标原点,则α= .
设曲线y=eax在点(0,1)处的切线与直线x+2y+1=0垂直,则a=________.
函数y=f(x)图象在M(1,f(1))处的切线方程为y=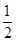 x+2,则f(1)+f′(1)
x+2,则f(1)+f′(1)
=________.
若曲线y=x2-1的一条切线平行于直线y=4x-3,则这条切线方程为_____________.
抛物线y=x2+x+2上点(1,4)处的切线的斜率是________,该切线方程为________________.
曲线f(x)=x2+3x在点A(2,10)处的切线的斜率为________.
曲线y=x2+2在点P(1,3)处的切线方程为________.
质点运动规律s=2t2+1,则从t=1到t=1+d时间段内运动距离对时间的变化率为________.